Вычисление определенных интегралов

Лабораторная работа

Вычисление определенных интегралов

1. Постановка задачи

Задача численного интегрирования функций заключается в вычислении приближенного значения определенного интеграла 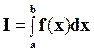. Определенный интеграл функции f(x) 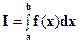численно равен площади криволинейной трапеции, ограниченной кривыми у=0, x=a, x=b, y=f(x) (рис. 1).

Рис. 1.

Метод средних прямоугольников

Для нахождения определенного интеграла методом средних прямоугольников площадь, ограниченная прямыми a и b, разбивается на n прямоугольников с одинаковыми основаниями h, высотами прямоугольников будут точки пересечения функции f(x) с серединами прямоугольников (h/2). Интеграл будет численно равен сумме площадей n прямоугольников (рис.2).

Рис. 2

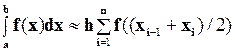, где 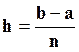-шаг интегрирования; n – количество шагов (интервалов).

Метод трапеций

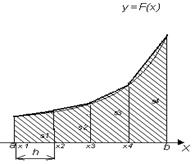
Для нахождения определенного интеграла методом трапеций площадь криволинейной трапеции разбивается на n прямоугольных трапеций с высотами h и основаниями у₀, у₁, у₂, у₃,..у_n, где n - номер прямоугольной трапеции. Интеграл будет приближенно равен сумме площадей прямоугольных трапеций (рис. 3).

Рис. 3

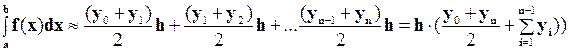(6)

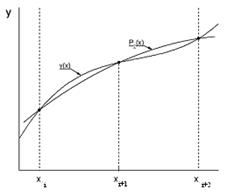
Метод Симпсона

Если для каждой пары отрезков

построить многочлен второй степени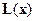

(рис.4)., затем проинтегрировать его на отрезке

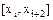и воспользоваться свойством аддитивности интеграла, то получим формулу Симпсона

Рис. 4 .

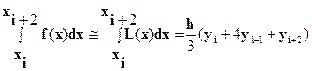Полученное для интеграла 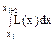значение совпадает с площадью криволинейной трапеции, ограниченной осью 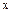, прямыми 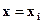, 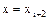и параболой, проходящей через точки На отрезке 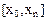формула Симпсона будет иметь вид:

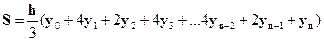
Число отрезков разбиения n является четным числом.

12 Следующая ⇒