Хелпикс

Главная

Контакты

Случайная статья



Распределения Рэлея и экспоненциальное распределение при расчёте показателей надёжности

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


17 Распределения Рэлея и экспоненциальное распределение при расчёте показателей надёжности

Экспоненциальное распределение – частный случай распределения Вейбулла, когда δ =1. Экспоненциальное распределение имеет единственный параметр λ. При экспоненциальном распределении времени отказов изделий интенсивность отказов λ(t) = λ=const

Вероятность безотказной работы Р(t)=e-λt

Средняя наработка до отказа Т=1/λ

Распределение Рэлея – частный случай распределения Вейбулла, когда δ = 2. Распределение Рэлея имеет единственный параметр δ*. При этом интенсивность отказов λ(t)=t/δ*2

Вероятность безотказной работы

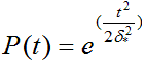
Средняя наработка до отказа

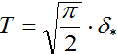
Задание.
1. Выпускаемое предприятием изделие имеет экспоненциальное распределение времени возникновения отказов при интенсивности отказов 3·10-5 1/ч. Вычислить вероятность безотказной работы на участке от 0 до 20000 ч с интервалами 500 ч и построить график Р(t). Рассчитать среднюю наработку до отказа.
2. Выпускаемое предприятием изделие имеет распределение Рэлея времени возникновения отказов при параметре распределения δ* = 1000 ч. Вычислить вероятность безотказной работы на участке от 10 до 1000 ч с интервалами 10 ч и построить графики Р(t) и λ(t). Рассчитать среднюю наработку до отказа.

 


18 Планирование испытаний методом однократной выборки

При планировании контрольных испытаний на надёжность методом однократной выборки определяют одноступенчатый план контроля, в который входят время испытаний tи, объем выборки n и приёмочное число C. Приёмочное число – это максимально возможное число отказавших за время испытания изделий, при котором партия изделий считается годной.

При планировании учитывают либо интересы поставщика и заказчика - планирование по приемочному и браковочному уровням, либо интересы только заказчика - планирование по браковочному уровню.

При планировании по приемочному и браковочному уровням задают:

1. Приемлемое значение вероятности безотказной работы случайно выбранного из партии изделия Pα.

2. Соответствующий ему риск поставщика α - вероятность того, что годная партия будет забракована.

3. Минимальное значение вероятности безотказной работы Pβ, т.е. браковочное (гарантированное) значение вероятности безотказной работы (всегда Pα > Pβ).

4. Соответствующий ему риск заказчика β - вероятность того, что бракованная партия будет признана годной.

При планировании по браковочному уровню задают Pβ и β. Планирование по браковочному уровню используют внутри предприятий-поставщиков, чтобы убедиться в соответствии надёжности требованиям заказчика.

В методе однократной выборки из партии берется одна выборка. Если в ней число отказавших изделий d <= C, партия принимается, иначе бракуется. При этом, если не известен закон распределения показателя надежности, время испытаний tи берут равным гарантированному времени tг, на которое задана минимальная вероятность безотказной работы Pβ.

Значения n и C находят следующим образом.

Вероятность P(Q) принять партию в зависимости от доли дефектных изделий в партии Q при определённых значениях С, N (объём партии) и n описывается гипергеометрическим распределением. При n <= 0,1N, что обычно и имеет место на практике, вместо гипергеометрического распределения с хорошим приближением можно использовать биномиальное, расчёты по которому проще.

При планировании по браковочному уровню для заданной Pβ подбирают такие значения n и C, чтобы P(Q), рассчитанная по биномиальному распределению, равнялась (была наиболее близка) риску поставщика β:

P(Q) = β (18.1)

Для конкретных заданных условий существует множество пар n и C, достаточно хорошо удовлетворяющих уравнению (18.1). Но C выбирают небольшим, поскольку при его увеличении резко возрастает объем выборки n. Однако обычно не принимают C = 0, поскольку это значение наиболее неблагоприятно для изготовителя.

При планировании по приемочному и браковочному уровням используют уравнение (18.1) и уравнение

P(Q) = 1 - α (18.2)

Подбирают n и C, чтобы одновременно выполнялись (18.1) и (18.2). При этом для конкретных заданных условий существует пара минимально возможных значений n и C, наиболее хорошо удовлетворяющих (18.1) и (18.2).

Пример 18.1. На предприятии необходимо провести испытания партии производимых изделий, чтобы убедиться в соответствии надёжности изделий требованиям заказчика, которые составляют: минимальная вероятность безотказной работы 0,92 на 300 ч при риске поставщика 0,1. Найти план контроля надежности.

Возможный вариант выполнения примера 18.1 показан на рис. 18.1.

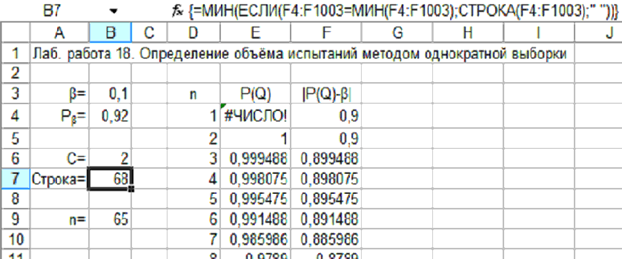
Рис. 18.1. Вариант расчёта для примера 18.1.

Вводим исходные данные Pβ и β, приёмочное число – например, 2 (потом при необходимости можно будет изменить это значение), а также столбец возможных значений объёма испытаний n (целесообразно хотя бы до 1000).

Теперь необходимо найти то из значений n, при котором выполняется условие (18.1). Для этого рассчитываем значения вероятности приёмки партии P(Q) в зависимости от объёма испытаний, используя функцию БИНОМРАСП. Диалоговое окно, открывающееся при выборе функции БИНОМРАСП, имеет четыре строки для ввода данных:

Число_успехов Судя по подсказке к этой строке, надо ввести количество успешных испытаний. Под количеством успешных испы-таний в данном случае понимается количество элементов выборки, имеющих определённый признак. В нашем случае это максимально возможное количество дефектных изделий в выборке, при котором партия принимается, т.е. следует сделать ссылку на ячейку со значе-нием приёмочного числа.

Число испытаний. Следует сделать ссылку на ячейку с величиной объёма испытаний (объёма выборки).

Вероятность_успеха. В нашем случае это вероятность того, что случайно выбранное из партии изделие будет бракованным, т.е. веро-ятность отказа, равная 1 - Pβ.

Интегральная. Поскольку партия принимается при любом ко-личестве дефектных изделий в выборке от 0 до С, то функция биномиального распределения должна быть интегральной, следовательно, вводится значение истина.

В тех случаях, когда n < C, расчёты по функции БИНОМРАСП дадут ошибку (получается значение #ЧИСЛО!). В то же время, очевидно, что в этих строках P(Q)=1.

Нужное значение n будет в той строке электронной таблицы, где P(Q) = β, точнее, где абсолютное значение P(Q) - β минимально, поэтому рассчитываем соответствующие значения. Но, поскольку при n < C расчёты P(Q) дают ошибку, используем функцию ЕСЛИ. При истинности логического условия n < C задаём значение 1 - β . При ложности логического условия находим модуль (функция ABS) P(Q) - β.

Получив столбец значений |P(Q)-β|, можно уже визуально найти в нём минимальное значение и соответствующий ему объём испытаний. Но для автоматизации расчётов следует найти нужный номер строки с использованием формулы массива, как это сделано в лабораторной работе № 2. Напоминание: чтобы введённая формула была формулой массива, нажимаем сочетание клавиш CTRL+SHIFT+ENTER (формула CSE), после чего формула будет заключена в фигурные скобки. При этом ввод фигурных скобок с клавиатуры не даст нужного результата. Кроме того, при каждом переводе курсора в строку формулы массива необходимо заново нажимать CTRL+SHIFT+ENTER, иначе формула уже не будет восприниматься как формула массива.

По номеру строки рассчитываем объем испытаний. Так, по рисунку 18.1, от найденного номера строки отнимаем 3, поскольку значения в столбцах начинаются только с четвёртой строки.

При приемочном числе 2 получаем необходимый объём испытаний 65. Таким образом, план контроля надёжности: n = 65, C = 2, tи = 300 ч.

Но можно задать любое другое приёмочное число и получить соответствующий ему объём испытаний.

Пример 18.2. Найти план контроля надёжности партии изделий по приемочному и браковочному уровням, если задано: Pα = 0,96, α = 0,1, Pβ = 0,92, β = 0,1 на 300 ч испытаний.

Возможный вариант выполнения примера 18.2 показан на рис. 18.2.

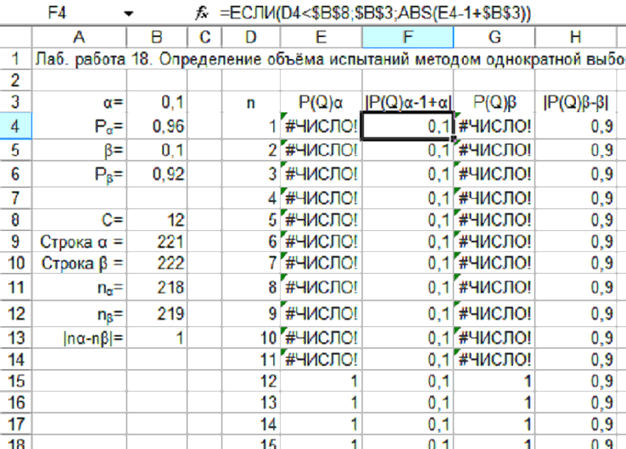
Рис. 18.2. Вариант расчёта для примера 18.2.

Вводим исходные данные Pα, α, Pβ и β, любое приёмочное число – например, 2 (потом это значение меняем), а также столбец возможных значений объёма испытаний n (целесообразно хотя бы до 4000). Рассчитываем столбцы значений P(Q)α, |P(Q)α-1+α|, P(Q)β, P(Q)β-β|. Значения Pα и Pβ рассчитываем с помощью функции БИНОМРАСП, при этом в диалоговом окне функции, в строке Вероятность_успеха, вводим 1 - Pα или 1 – Pβ, в зависимости от столбца. Далее при помощи формул массива, в соответствии с (18.1) и (18.2), находим номера строк, в которых соответственно абсолютные значения P(Q)α-1+α и P(Q)β - β минимальны (наиболее близки к нулю). По этим номерам строк находим объёмы выборок nα и nβ, обеспечивающих заданные α и β, а также модуль разности между ними. Затем подбираем такое значение приёмочного числа (минимальное из возможных), чтобы этот модуль разности был минимален (чаще всего от 0 до 4). В план контроля надёжности (план испытаний) войдут подобранное значение приёмочного числа и одно из найденных значений nα и nβ или одно из промежуточных между ними значений. Можно принять в качестве объёма испытаний n среднее между nα и nβ. При этом реальные риски поставщика и потребителя будут несколько отличаться от заданных.

В нашем примере получим план контроля надёжности: n = 218, C = 12, tи = 300 ч.

Задание.
1. Выполнить расчёты в соответствии с примером 18.1 при различных значениях приёмочного числа, минимальной вероятности безотказной работы и риска потребителя, указанных в табл. 18.1. Результаты занести в таблицу 18.1 на отдельном листе электронной книги. Сделать выводы о том, как влияют на объём испытаний увеличение приёмочного числа, минимальной вероятности безотказной работы и риска потребителя.

Таблица 18.1.

Приёмочное число

Pβ

Объём испытаний
β=0,05 β=0,1 β=0,2
0,92      
0,94      
0,92      
0,94      
0,92      
0,94      
0,92      
0,94      

2. Выполнить расчёты в соответствии с примером 18.2 при различных значениях приемлемой вероятности безотказной работы, минимальной вероятности безотказной работы, риска изготовителя и риска потребителя, указанных в табл. 18.2. Результаты занести в таблицу 18.2 на отдельном листе электронной книги. Сделать выводы о том, как влияют на объём испытаний и приёмочное число увеличение приемлемой вероятности безотказной работы, минимальной вероятности безотказной работы, риска изготовителя и риска потребителя.

Таблица 18.2.

Pα

Pβ

α=β=0,05

α=β=0,1

α=β=0,2
n C n C n C

0,94

 0,90            
0,91            

0,95

 0,90            
0,91            

 



⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.