КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА-КАИ

Стр 1 из 4Следующая ⇒

Министерство образования и науки РФ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

КАЗАНСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ им. А.Н.ТУПОЛЕВА-КАИ

Учебное пособие по выполнению лабораторных работ по испытаниям

Казань 2016

Составители: доцент И.А. Горбунов, проф. Ф.А. Карамов

УДК

Учебное пособие по выполнению лабораторных работ/Казан. нац. исслед. техн. ун-т; Сост. доцент И.А. Горбунов, проф. Карамов Ф.А., Казань, 2015 г./.

Пособие предназначено для проведения лабораторных работ с использованием ИК-Фурье спектрофотометра для получения спектральных характеристик (спектрограмм) материалов электроники в ближней, средней и дальней ИК-областях.

Табл. __. Ил. __. Библиограф.: __ назв.

ИСПЫТАНИЯ НА НАДЁЖНОСТЬ

15 Определение показателей безотказности по опытным данным

Надежность – это свойство объекта сохранять во времени в установленных пределах значения необходимых параметров. Надёжность включает в себя безотказность, долговечность, ремонтопригод-ность и сохраняемость.

Основные показатели безотказности для невосстанавливаемых объектов: вероятность безотказной работы, средняя наработка до отказа (среднее время безотказной работы), интенсивность отказов.

Вероятность безотказной работы P(t) - это вероятность того, что в пределах заданного времени отказ объекта не возникнет.

P(t) = (n₀ - n(t))/n₀

Здесь n₀ – начальное число работоспособных изделий, n(t) - число изделий, отказавших за время t.

Иногда используют понятие вероятность отказа Q(t):

Q(t) = 1- P(t)

Интенсивность отказов Λ(t), ч^-1, показывает, какая доля исправных в начальный момент рассматриваемого промежутка времени изделий в выборке отказывает к концу этого промежутка.

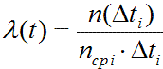
Здесь n(Δt_i) – число отказов в интервале Δt_i), n_ср_i – число работоспособных изделий в середине интервала:

n_ср_i= n₀ - n(t) + n(Δt_i)/2

Кривая Λ(t) (лямбда-характеристика) часто имеет вид, показанный на рис. 15.1.

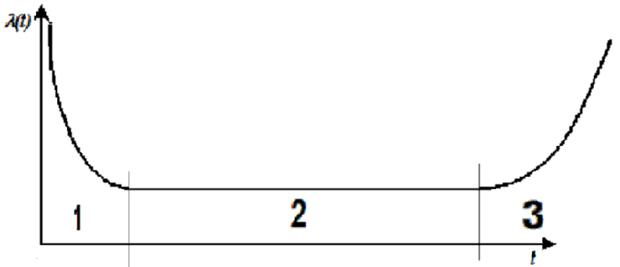
Рис. 15.1. Лямбда-характеристика

На рис. 15.1 область 1 - период приработки изделий, который характеризуется высокой интенсивностью отказов из-за наличия скрытых дефектов. 2 - рабочая область (нормальная эксплуатация), в которой интенсивность отказов почти постоянна. 3 - область износа, в которой интенсивность отказов резко возрастает из-за износа и старения изделий.

Средняя наработка до отказа, или среднее время безотказной работы – это математическое ожидание наработки изделий до первого отказа:

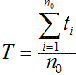
Здесь n₀ – начальное число работоспособных изделий, t_i - время наработки i-го изделия до первого отказа.

При λ(t)=const
T=1/ λ(t) (15.1)

Пример 15.1. На испытании находилось n₀ = 1000 экземпляров невосстанавливаемого радиоэлектронного устройства. Через каждые 100 часов фиксировались отказы. Число отказов n(Δt_i) в каждом интервале Δt_i показано в табл. 15.1.Найти вероятность безотказной работы P(t) и интенсивность отказов λ(t) в интервале от 0 до 2000 часов. Построить графики P(t) и λ(t). Найти среднюю наработку до отказа.

Таблица 15.1.

Номер интервала i
Интервал λ(t), ч	0..100	100..200	200..300	300..400	400..500	500..600	600..700	700..800	800..900	900..1000
Число отказов n(Δt_i)
Номер интервала i

Интервал λ(t), ч	1000..1100	1100..1200	1200..1300	1300..1400	1400..1500
1500..1600	1600..1700	1700..1800	1800..1900	1900..2000
Число отказов n(Δt_i)

Фрагмент расчёта для примера 15.1 показан на рис. 15.2.

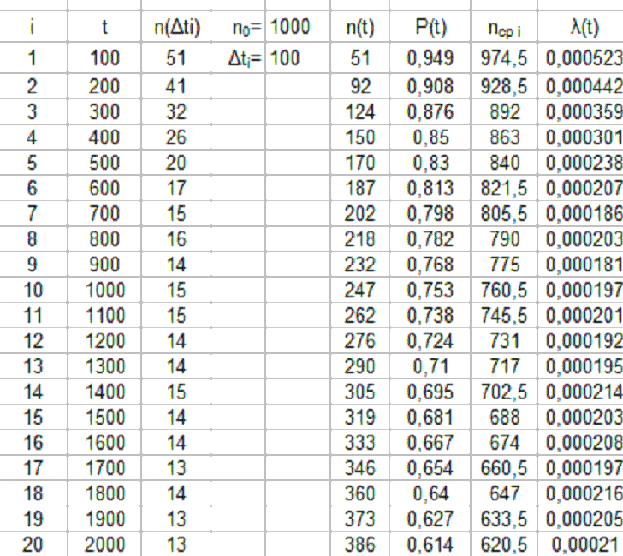
Рис. 15.2. Фрагмент расчёта для примера 15.1.

Вводим столбцы исходных данных: номера интервалов, время концов интервалов, число отказов в интервалах. Вводим также начальное число работоспособных изделий и продолжительность одного интервала.

Рассчитываем столбец n(t) - число изделий, отказавших после начала испытаний. Для этого в первую ячейку столбца вводим 51, т.е. число изделий, отказавших к концу первого интервала. В следующей ячейке находим число изделий, отказавших к концу второго интервала, суммируя значение в предыдущей ячейке и число отказов во втором интервале. Полученную формулу из этой ячейки копируем в остальные ячейки столбца. Далее находим значения вероятностей безотказной работы, числа работоспособных изделий в середине интер-вала и интенсивностей отказов.

Строим графики P(t) и λ(t). При построении графиков на шаге Вид диаграммы выбираем Точечная диаграмма – на которой значения соединены отрезками. На втором шаге выбираем вкладку Ряд, добавляем один ряд и вводим необходимые диапазоны значений по X и по Y. На третьем шаге вводим заголовки и отменяем легенду. Полученную диаграмму редактируем при помощи контекстного меню и двойного клика мышью на редактируемых элементах диаграммы.

График λ(t) показан на рис. 15.3.

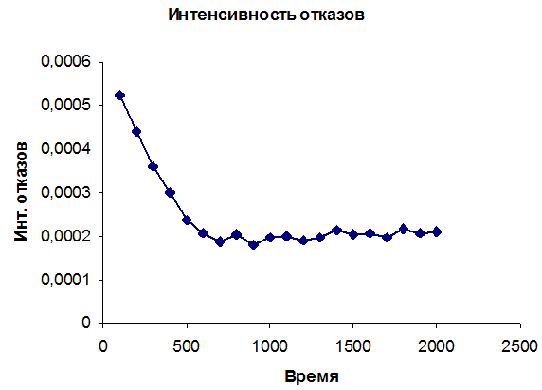
Рис.15.3. График интенсивности отказов.

Как видно из графика, после периода приработки, составляющего около 600 часов, интенсивность отказов становится практически постоянной, т.е. можно считать, что λ(t)=const. Поэтому рассчитываем среднюю наработку до отказа по уравнению 15.1. Для этого постоянное значение интенсивности отказов находим как среднее по интервалам от 6 до 20.

Задание.
1. Выполнить пример 15.1.

12 3 4 Следующая ⇒