
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Краткие теоретические сведения:
Краткие теоретические сведения:
Предел последовательности
Определение.Число 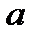 называется пределом последовательности
называется пределом последовательности 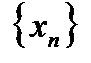 , если для любого положительно
, если для любого положительно 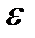 го числа найдется такое натуральное число
го числа найдется такое натуральное число 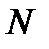 , что при всех
, что при всех 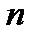 >
> 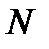 выполняетсянеравенство
выполняетсянеравенство 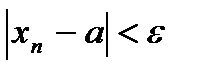
Пишут: 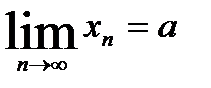

Графически это выглядит так:
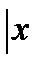 n -
n - 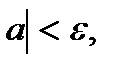

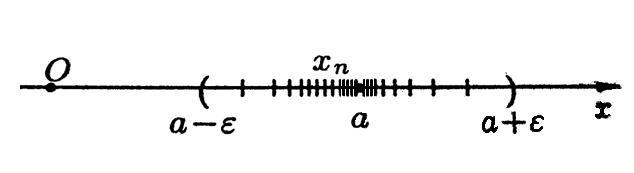
Т.е. элемент 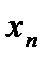 находится в
находится в 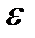 - окрестности точки а. При этом последовательности
- окрестности точки а. При этом последовательности 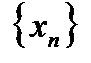 называется сходящейся, в противном случае – расходящейся.
называется сходящейся, в противном случае – расходящейся.
Основные свойства сходящихся последовательностей
1)Сходящаяся последовательность ограничена.
2)Пусть  ,
, 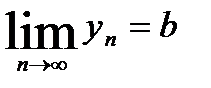 , тогда а)
, тогда а) 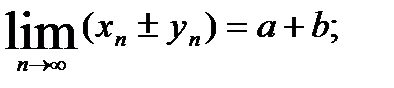 б)
б) 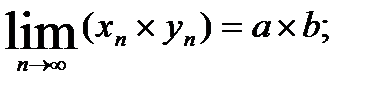 в)
в) 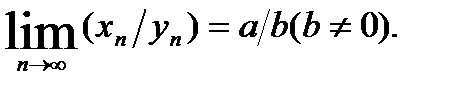
3)Если 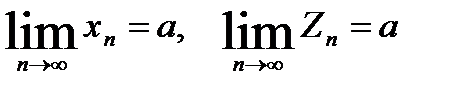 и для всех
и для всех 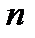 выполняется неравенства
выполняется неравенства 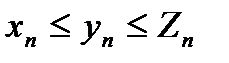 , то
, то  .
. 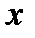
4) Если 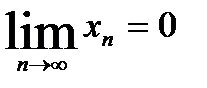 и последовательность {уn}- ограниченная, то
и последовательность {уn}- ограниченная, то 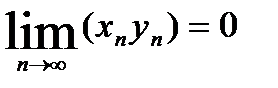
| №1. Найти пределы: | |
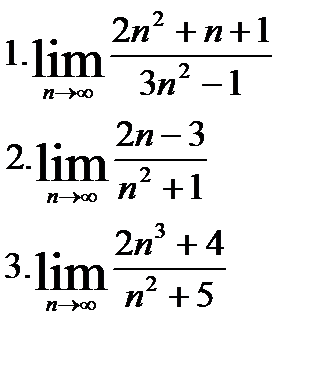

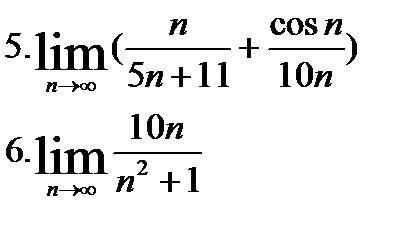
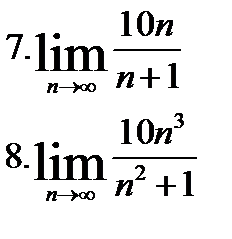


| 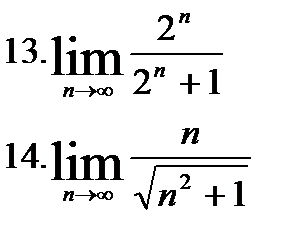
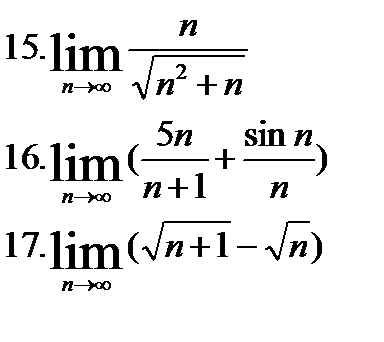
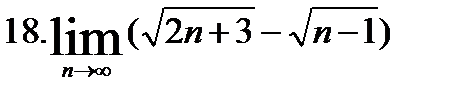
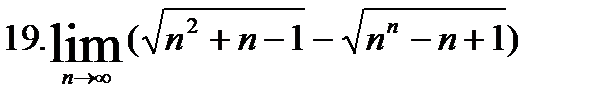
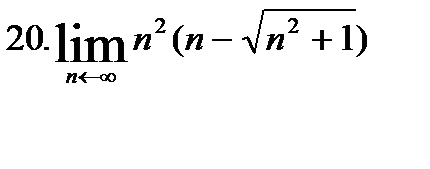
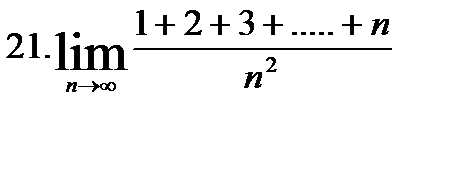
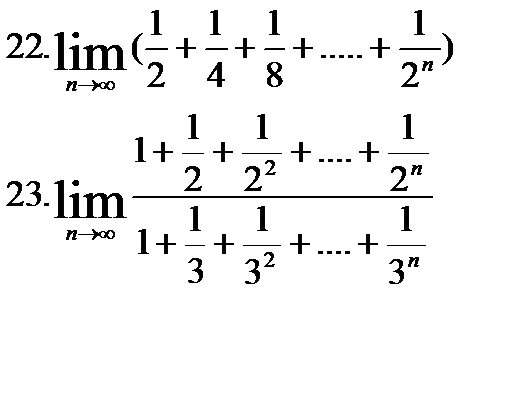
|
Бесконечно большие и бесконечно малые функции
Определение.Функция 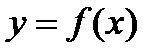 называется бесконечно малой при
называется бесконечно малой при  , если
, если 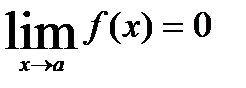
Например: 1) 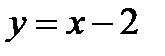 при
при 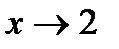 б. м. ф. т.к.
б. м. ф. т.к. 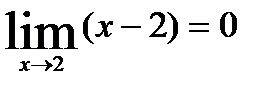 2)
2)  при
при 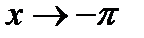 б. м. ф. т. к
б. м. ф. т. к 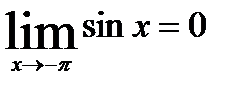
Определение.Функция 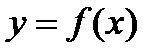 называется бесконечно большой при
называется бесконечно большой при 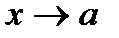 , если
, если 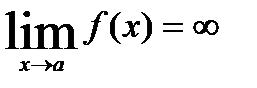 ,
, 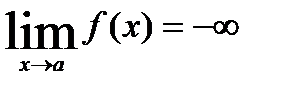 или
или 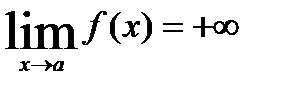
Например,  есть б. б. Ф при
есть б. б. Ф при 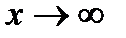 ;
; 
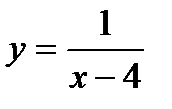 если б. б. ф. при
если б. б. ф. при  действительно
действительно 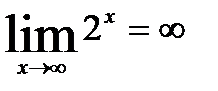 и
и 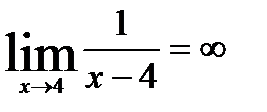
Теорема (о связи между функций, ее приделом и бесконечно малой функцией). Если функция 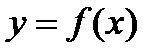 имеет придел, равный
имеет придел, равный  , то ее можно представить как сумму числа
, то ее можно представить как сумму числа  и бесконечно малой функции
и бесконечно малой функции  , т.е. если
, т.е. если 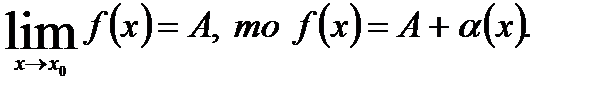
Теорема (обратная). Если функцию 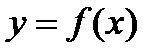 можно представить в виде суммы числа А и б.м.ф.
можно представить в виде суммы числа А и б.м.ф. 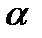 (x), то число А является пределом функции
(x), то число А является пределом функции 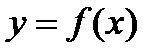 , т.е если
, т.е если 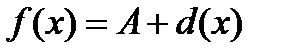 , то
, то 
Например, требуется вычислить 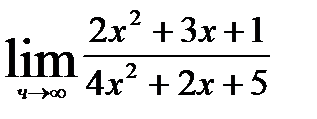 . Представим числитель и знаменатель в виде суммы числа и б.м.ф.
. Представим числитель и знаменатель в виде суммы числа и б.м.ф. 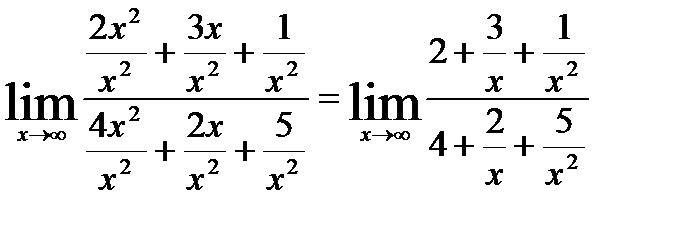
Функции 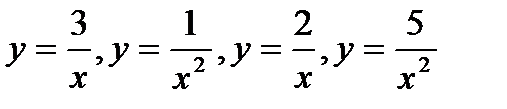 при
при 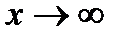 есть б.м.ф. таким образом
есть б.м.ф. таким образом 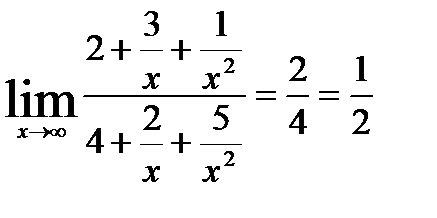
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|