
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вывод формул. Примеры использования
Вывод формул
Для вывода формул суммы и разности синусов можно использовать формулы сложения, в частности, формулы
синуса суммы 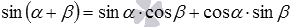 ,
,
синуса разности 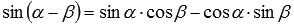 ,
,
косинуса суммы 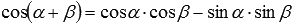 и
и
косинуса разности 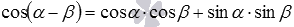 .
.
Также нам потребуется представление углов 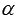 и
и 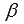 в виде
в виде 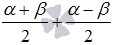 и
и 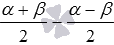 . Такое представление правомерно, так как
. Такое представление правомерно, так как  и
и 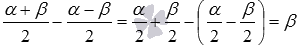 для любых углов
для любых углов 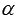 и
и 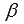 .
.
Теперь подробно разберем вывод формулы суммы синусов двух углов вида 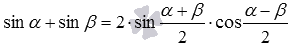 .
.
Сначала в сумме 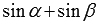 заменяем
заменяем  на
на 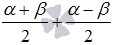 , а
, а  на
на 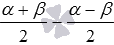 , при этом получаем
, при этом получаем 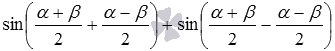 . Теперь к
. Теперь к 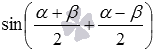 применяем формулу синуса суммы, а к
применяем формулу синуса суммы, а к 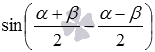 - формулу синуса разности:
- формулу синуса разности:
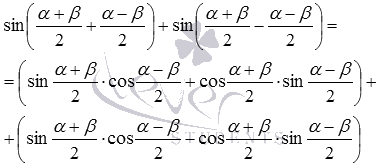
После приведения подобных слагаемых получаем 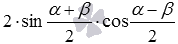 . В итоге имеем формулу суммы синусов вида
. В итоге имеем формулу суммы синусов вида 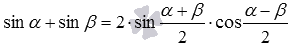 .
.
Для вывода остальных формул нужно лишь проделать аналогичные действия. Приведем вывод формул разности синусов, а также суммы и разности косинусов:
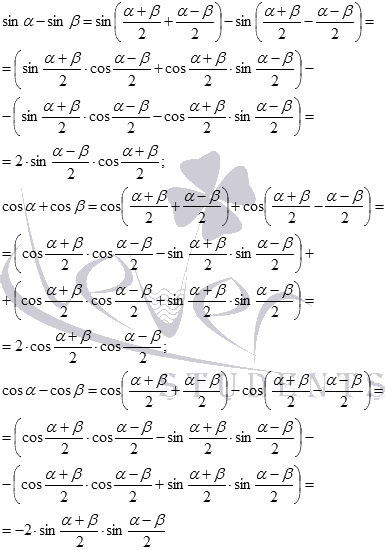
Для разности косинусов мы привели формулы двух видов 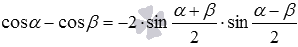 или
или 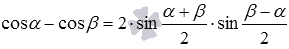 . Они эквивалентны, так как
. Они эквивалентны, так как 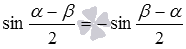 , что следует из свойств синусов противоположных углов.
, что следует из свойств синусов противоположных углов.
Итак, мы разобрали доказательство всех формул суммы и разности синусов и косинусов.
Примеры использования
Разберем несколько примеров использования формул суммы синусов и косинусов, а также разности синусов и косинусов.
Для примера проверим справедливость формулы суммы синусов вида 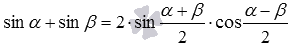 , взяв
, взяв 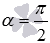 и
и 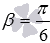 . Чтобы это сделать, вычислим значения левой и правой частей формулы для данных углов. Так как
. Чтобы это сделать, вычислим значения левой и правой частей формулы для данных углов. Так как 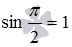 и
и 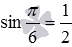 (при необходимости смотрите таблицу основных значений синусов и косинусов), то
(при необходимости смотрите таблицу основных значений синусов и косинусов), то 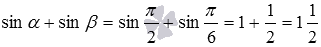 . При
. При 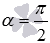 и
и 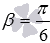 имеем
имеем 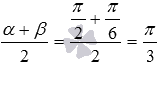 и
и 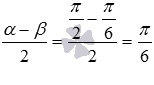 , тогда . Таким образом, значения левой и правой частей формулы суммы синусов для
, тогда . Таким образом, значения левой и правой частей формулы суммы синусов для 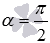 и
и 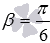 совпадают, что подтверждает справедливость этой формулы.
совпадают, что подтверждает справедливость этой формулы.
В некоторых случаях использование формул суммы и разности синусов и косинусов позволяет вычислять значения тригонометрических выражений, когда углы отличны от основных углов (  ). Приведем решение примера, подтверждающего эту мысль.
). Приведем решение примера, подтверждающего эту мысль.
Пример.
Вычислите точное значение разности синусов 165 и 75 градусов.
Решение.
Точных значений синусов 165 и 75 градусов мы не знаем, поэтому непосредственно вычислить значение заданной разности мы не можем. Но ответить на вопрос задачи нам позволяет формула разности синусов 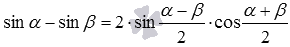 . Действительно, полусумма углов 165 и 75 градусов равна 120, а полуразность равна 45, а точные значения синуса 45 градусов и косинуса 120 градусов известны.
. Действительно, полусумма углов 165 и 75 градусов равна 120, а полуразность равна 45, а точные значения синуса 45 градусов и косинуса 120 градусов известны.
Таким образом, имеем
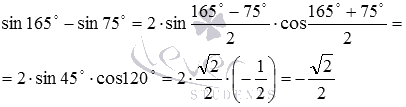
Ответ:
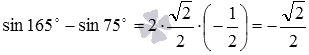 .
.
Несомненно, главная ценность формул суммы и разности синусов и косинусов заключается в том, что они позволяют перейти от суммы и разности к произведению тригонометрических функций (по этой причине эти формулы часто называют формулами перехода от суммы к произведению тригонометрических функций). А это в свою очередь может быть полезно, например, при преобразовании тригонометрических выражений или при решении тригонометрический уравнений. Но эти темы требуют отдельного разговора.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|