
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сумма и разность синусов и косинусов, вывод формул, примеры.
Сумма и разность синусов и косинусов, вывод формул, примеры.
В продолжение темы тригонометрические формулы рассмотрим формулы суммы и разности синусов и косинусов (не путать с формулами синуса и косинуса суммы и разности). Эти формулы позволяют от суммы или разности синусов и косинусов углов 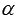 и
и 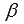 перейти к произведению синусов и/или косинусов углов
перейти к произведению синусов и/или косинусов углов 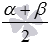 и
и 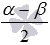 . В этой статье мы сначала перечислим эти формулы, дальше покажем их вывод, а в заключение рассмотрим несколько примеров их применения.
. В этой статье мы сначала перечислим эти формулы, дальше покажем их вывод, а в заключение рассмотрим несколько примеров их применения.
Список формул
Запишем формулы суммы и разности синусов и косинусов. Как Вы понимаете, их четыре штуки: две для синусов и две для косинусов.
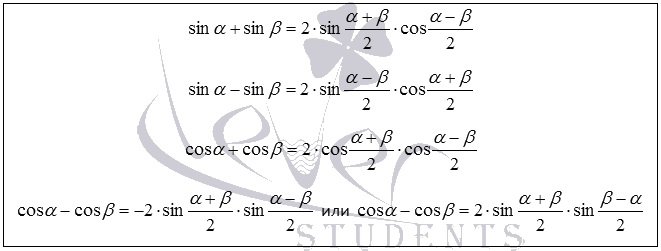
Теперь дадим их формулировки. При формулировании формул суммы и разности синусов и косинусов угол 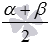 называют полусуммой углов
называют полусуммой углов 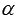 и
и 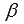 , а угол
, а угол 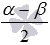 - полуразностью. Итак,
- полуразностью. Итак,
- Формула суммы синусов
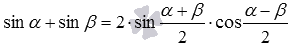 : сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности.
: сумма синусов двух углов равна удвоенному произведению синуса полусуммы этих углов на косинус их полуразности. - Формула разности синусов
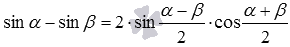 : разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы.
: разность синусов двух углов равна удвоенному произведению синуса полуразности этих углов на косинус их полусуммы. - Сумма косинусов
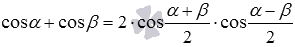 : сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов.
: сумма косинусов двух углов равна удвоенному произведению косинуса полусуммы на косинус полуразности этих углов. - Формула разности косинусов
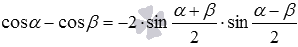 : разность косинусов двух углов равна удвоенному произведению синуса полусуммы на синус полуразности этих углов, взятому со знаком минус.
: разность косинусов двух углов равна удвоенному произведению синуса полусуммы на синус полуразности этих углов, взятому со знаком минус.
Стоит отметить, что формулы суммы и разности синусов и косинусов справедливы для любых углов 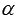 и
и 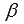 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|