
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Упражнения. Тема 2. Бесконечные пределы.. Бесконечно малые. и бесконечно большие пределы. Упражнения. Тема 3. Замечательные пределы.. Применение их при вычислении пределов. Упражнения. Дополнительно. Зачетная работа. по теме «Предел функции»
Упражнения
1. 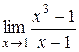 ; 13.
; 13. 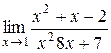 ;
;
2. 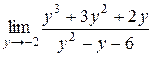 ; 14.
; 14. 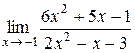 ;
;
3. 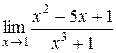 ; 15.
; 15. 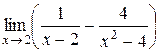 ;
;
4.  ; 16.
; 16. 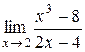 ;
;
5. 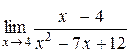 ; 17.
; 17. 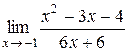 ;
;
6. 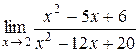 ; 18.
; 18. 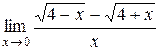 ;
;
7. 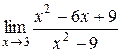 ; 19.
; 19. 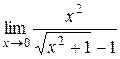 ;
;
8. 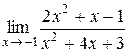 ; 20.
; 20. 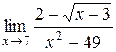 ;
;
9. 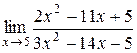 ; 21.
; 21. 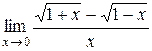 ;
;
10. 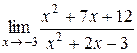 ; 22.
; 22. 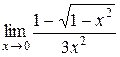 ;
;
11.  ; 23.
; 23.  ;
;
12. 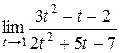 ; 24.
; 24. 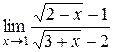 ;
;
25. 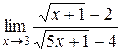 ; 29.
; 29. 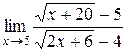 ;
;
26.  ; 30.
; 30. 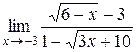 ;
;
27. 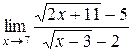 ; 31.
; 31. 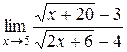 ;
;
28.  ; 32.
; 32. 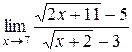 .
.
Тема 2. Бесконечные пределы.
Бесконечно малые
и бесконечно большие пределы
df: Функция 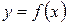 называется бесконечно малой при
называется бесконечно малой при 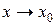 , если
, если 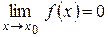 .
.
Например:
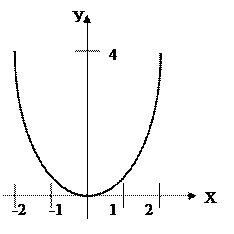 1)
1) 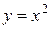
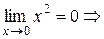
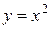 - бесконечно малая функция
- бесконечно малая функция
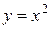
2) 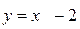
 - бесконечно малая функция
- бесконечно малая функция
 |
df: Функция 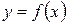 называется бесконечно большой при
называется бесконечно большой при 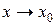 если для любого числа
если для любого числа 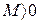 найдется такое
найдется такое 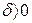 , что при
, что при 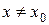 имеет место
имеет место
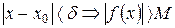 ;
;
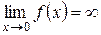 .
.
Например, 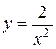


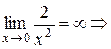
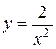 – бесконечно большая функция
– бесконечно большая функция
Предел вида 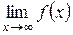 называется бесконечным пределом.
называется бесконечным пределом.
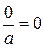 ;
;  ;
; 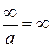 .
.
Например
1) 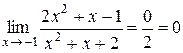 ;
;
2) 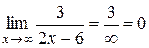 ;
;
3) 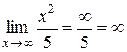 ;
;
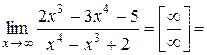
Чтобы решить предел такого вида нужно избавиться от неопределенности 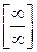 . Для этого и числитель и знаменатель необходимо разделить на
. Для этого и числитель и знаменатель необходимо разделить на 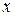 в наивысшей степени знаменателя
в наивысшей степени знаменателя 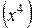 .
.
 .
.
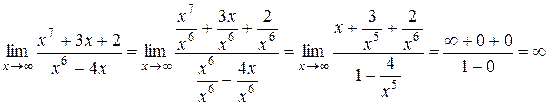 .
.
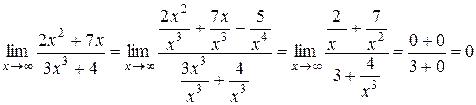 .
.
Упражнения
№1. 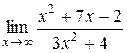 ; №2.
; №2. 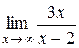 ;
;
№3. 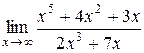 ; №4.
; №4. 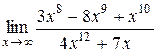 ;
;
№5. 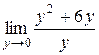 ; №6.
; №6. 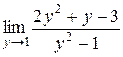 ;
;
№7. 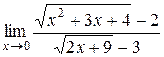 ; №8.
; №8.  ;
;
№9.  ; №10.
; №10. 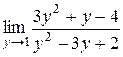 ;
;
№11. 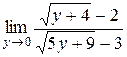 ; №12.
; №12. 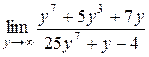 ;
;
№13. 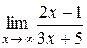 ; №14.
; №14. 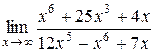 ;
;
№15.  ; №16.
; №16. 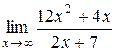 ;
;
№17. 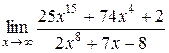 ; №18.
; №18. 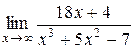 ;
;
№19.  ; №20.
; №20.  .
.
Тема 3. Замечательные пределы.
Применение их при вычислении пределов
I. При вычислении пределов, содержащих тригонометрические функции, часто используют предел
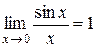
| или | 
|
называемый первым замечательным пределов.
Читается: предел отношения синуса к его аргументу равен единице, когда аргумент стремится к нулю.
1) 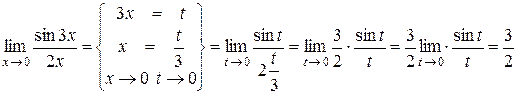 .
.
2) 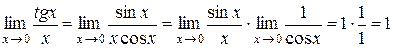 .
.
3) 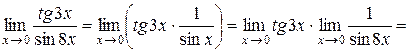
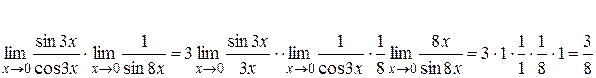
4) 
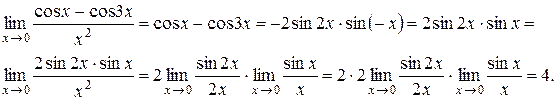
5) 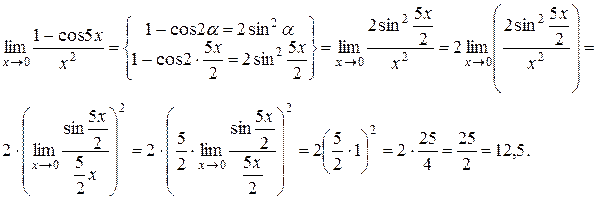
6) 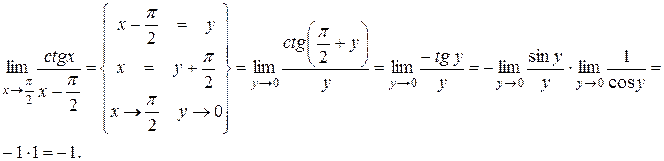
II. Второй замечательный предел
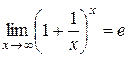
| 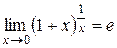
|
1) 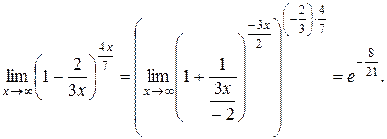
2) 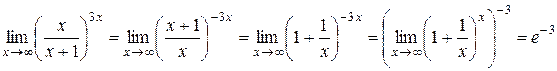 .
.
3) 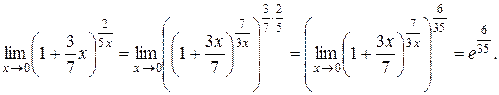
Упражнения
1. 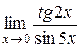 ; 2.
; 2. 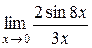 ; 3.
; 3.  ;
;
4. 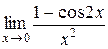 ; 5.
; 5. 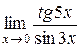 ; 6.
; 6. 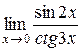 ;
;
7. 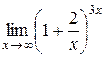 ; 8.
; 8.  ; 9.
; 9.  ;
;
10. 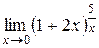 ; 11.
; 11.  ; 12.
; 12. 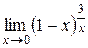 ;
;
13. 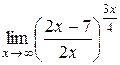 ; 14.
; 14. 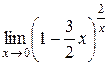 .
.
Дополнительно
1. 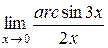 ; 2.
; 2.  ; 3.
; 3. 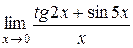 ;
;
4. 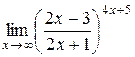 ; 5.
; 5.  ; 6.
; 6. 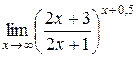 .
.
Зачетная работа
по теме «Предел функции»
1. 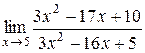 ;
;
2. 
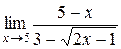 ;
;
3. 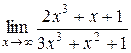
4. 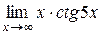 ;
;
5. 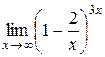 ;
;
6. 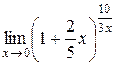 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|