
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Р А З Д Е Л II. ТЕОРИЯ ПРЕДЕЛОВ ФУНКЦИИ. Тема 1. Предел функции в точке.. Теорема о пределах. Основные теоремы о пределах
Р А З Д Е Л II
ТЕОРИЯ ПРЕДЕЛОВ ФУНКЦИИ
Тема 1. Предел функции в точке.
Теорема о пределах
Дана функция 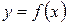 ,
, 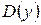 ,
, 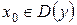
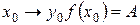 ;
;
при условии 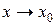 выполняется условие
выполняется условие 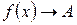 т.е.
т.е. 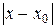 – уменьшается
– уменьшается 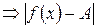 – уменьшается.
– уменьшается.
Определение: Число 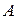 называется пределом функции
называется пределом функции 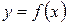 в точке
в точке 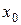 (или при
(или при 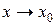 ), если для любого
), если для любого 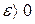 существует такое
существует такое 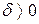 , что для всех
, что для всех 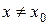 удовлетворяющих неравенству
удовлетворяющих неравенству 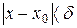 , выполняется неравенство
, выполняется неравенство 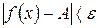 .
.
Обозначим 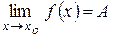 ;
;
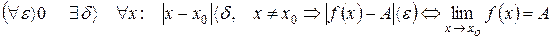 .
.
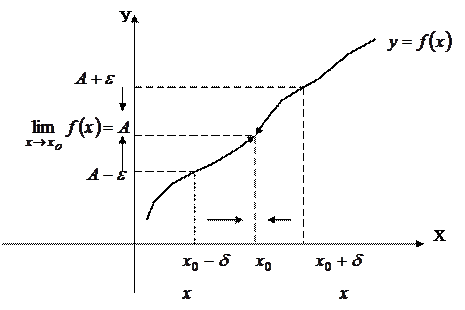 |
Рис. 1. Геометрическая иллюстрация предела функции
Основные теоремы о пределах
Теорема 1. Предел суммы (разности) функций
равен сумме (разности) их пределов
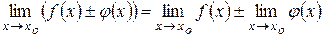 .
.
Например: 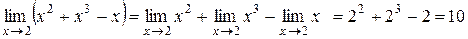 .
.
Следствие: функция может иметь только один предел при 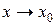 .
.
Теорема 2. Предел произведения двух функций
равен произведению их пределов
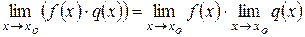 .
.
Например: 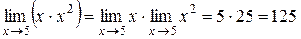 .
.
Следствие:
1. Постоянный множитель можно выносить за знак предела.
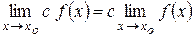 .
.
Например: 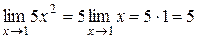 .
.
2. Предел степени с натуральным показателем равен
той же степени предела.
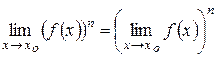 ;
;
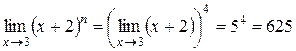 .
.
Теорема 3. Предел отношения, равен отношению пределов
при условии, что предел знаменателя отличен от нуля.
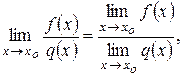
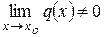 .
.
1). 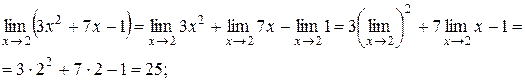
Таким образом, для вычисления предела многочлена 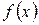 при
при 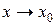 достаточно вместо переменной
достаточно вместо переменной 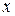 подставить значение
подставить значение 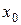 , к которому она стремиться, и выполнить соответствующие действия, т.е.
, к которому она стремиться, и выполнить соответствующие действия, т.е.
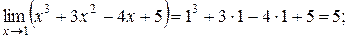
2) 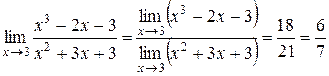 .
.
3) Рассмотрим решения пределов, когда предел знаменателя дроби обращается в ноль.
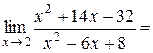 .
.
При постановке «2» вместо переменной 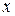 в числителе и в знаменателе дроби получается ноль. В таких случаях говорят, что имеем неопределенность вида
в числителе и в знаменателе дроби получается ноль. В таких случаях говорят, что имеем неопределенность вида 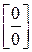 . Чтобы решить предел такого вида нужно числитель и знаменатель разложить на множители.
. Чтобы решить предел такого вида нужно числитель и знаменатель разложить на множители.
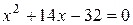
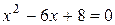
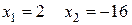
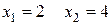
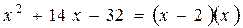
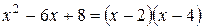 .
.
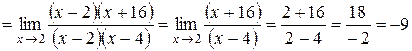 .
.
4) 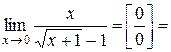
Чтобы решить предел такого вида необходимо избавиться от неопределенности, для этого числитель и знаменатель умножают на выражение, сопряженное знаменателю, т.е. 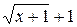
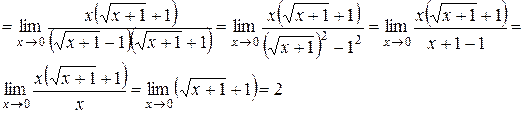 .
.
5) 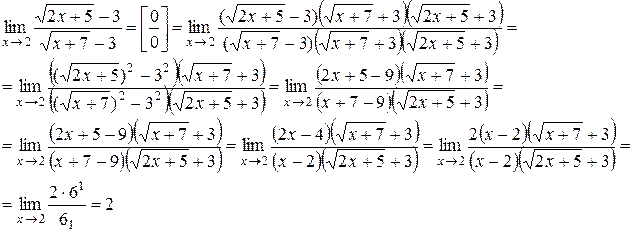 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|