Предел функции (некоторые правила вычисления пределов)

⇐ ПредыдущаяСтр 2 из 3Следующая ⇒

Ответ. 1;1;3;5;11.

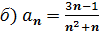
В данную формулу вместо n подставить сначала 1, потом 2, 3 ит.д. до n=6.

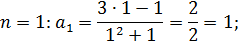
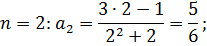
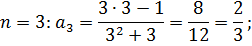
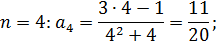
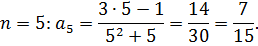
Ответ.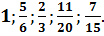

Пример №2.Дана арифметическая прогрессия {a_n}: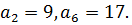

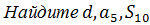
Решение.

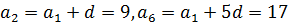
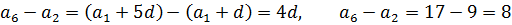
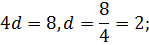
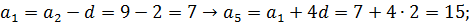
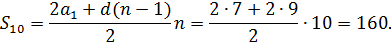
Ответ.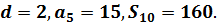

Предел функции (некоторые правила вычисления пределов)

1.Итак, первое правило:Когда дан любой предел, сначала просто пытаемся подставить число в функцию.

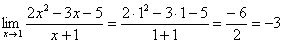
2. Пределы с неопределенностью вида и метод их решения

Итак, метод решения следующий: для того, чтобы раскрыть неопределенностьнеобходимо разделить числитель и знаменатель на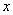 в старшей степени.

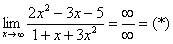
Разделим числитель и знаменатель на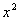

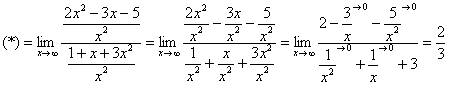
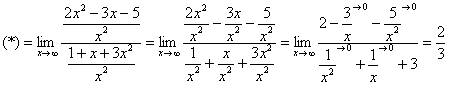
Некоторые примеры вычисления пределов:

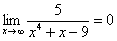
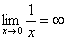
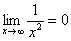
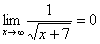
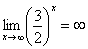
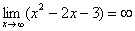
3. Пределы с неопределенностью вида 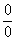и метод их решения

А) Общее правило: если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида 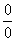, то для ее раскрытия нужно разложить числитель и знаменатель на множители.

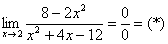
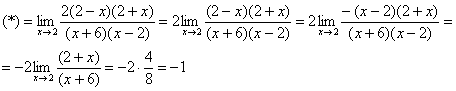
Б) Метод умножения числителя и знаменателя на сопряженное выражение

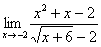
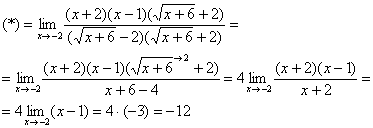
Пример № 3. Вычислите пределы функций

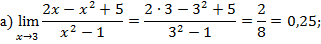
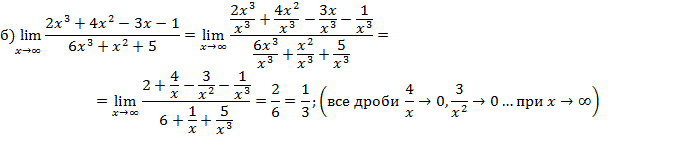
Порядок выполнения работы.

Задание 1.Внимательно разберите Примеры №1 и №2, перепишите их в тетради; рассмотрите примеры нахождения пределов функции (их переписывать не нужно).

Задание №2. Решите самостоятельную работу по образцу(см.Примеры №1 и №2)- решение прислать в личных сообщениях фотографиями. Все работы подписываем

Номера вариантов для выполнения самостоятельной работы:

ФИО	Задание №1
Гумеров А.
Нафиков Д.
Рогов И.
Сагадатгареев Р.
Семенов В.
Шарапов И.
Тихонов В.
Большаков Г.
Гамбаров А.
Гильманова Д.
Ефимов И.
Гилязев А.
Кузнецов А.
Наумов Д.
Расулов М.
Султанмуратов Т.
Шафиев И.
Фазыляхметова Р.

⇐ Предыдущая 123 Следующая ⇒