I. ПРЕДЕЛЫ. Теоретические вопросы

I. ПРЕДЕЛЫ

Теоретические вопросы

1. Понятие числовой последовательности и ее предела. Теорема об ограниченности сходящейся последовательности.

2. Понятие предела функции в точке. Понятие функции, ограниченной в окрестности точки. Теорема об ограниченности функции, имеющей предел.

3. Теорема о переходе к пределу в неравенствах.

4. Теорема о пределе промежуточной функции.

5. Понятие непрерывности функции. Доказать непрерывность функции .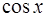

6. Первый замечательный предел .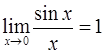

7. Понятие бесконечно малой функции. Теорема о связи между функцией, ее пределом и бесконечно малой.

8. Теорема о сумме бесконечно малых функций.

9. Теорема о произведении бесконечно малой функции на ограниченную функцию.

10. Теорема об отношении бесконечно малой функции к функции, имеющей предел, отличный от нуля.

11. Теорема о пределе суммы.

12. Теорема о пределе произведения.

13. Теорема о пределе частного.

14. Теорема о переходе к пределу под знаком непрерывной функции.

15. Непрерывность суммы, произведения и частного.

16. Непрерывность сложной функции.

17. Понятие бесконечно большой функции. Теоремы о связи бесконечно больших функций с бесконечно малыми.

18. Сравнение бесконечно малых функций.

19. Эквивалентные бесконечно малые функции. Теорема о замене бесконечно малых функций эквивалентными.

20. Условие эквивалентности бесконечно малых функций.