Среднее время жизни. Бк = 1 распад/c

Среднее время жизни

Из закона радиоактивного распада можно получить выражение для среднего времени жизни радиоактивного атома. Число атомов, в момент времени 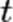претерпевших распад в пределах интервала 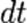равно 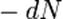, их время жизни равно 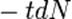. Среднее время жизни получаем интегрированием по всему периоду распада:

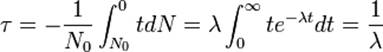
Подставляя эту величину в экспоненциальные временные зависимости для N(t) и I(t), можно заметить, что за время τ число радиоактивных атомов и скорость их распада уменьшаются в e раз[

Активность A -среднее количество ядер распадающихся в единицу времени

A(t) = λN(t)

Активность измеряется в кюри (Ки) и беккерелях (Бк)

1 Ки = 3.7·10¹⁰распадов/c,

1 Бк = 1 распад/c

Распад исходного ядра 1 в ядро 2, с последующим его распадом в ядро 3, описывается системой дифференциальных уравнений

dN₁/dt = - λ₁N₁

dN₂/dt = - λ₂N₂ + λ₁N₁

где N₁(t) и N₂(t) - количество ядер, а λ₁ и λ₂ - постоянные распада ядер 1 и 2 соответственно. Решением данной системы с начальными условиями

N₁(0) = N₁₀; N₂(0) = 0 будет

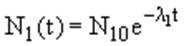
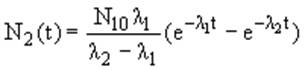
Количество ядер 2 достигает максимального значения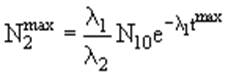

при

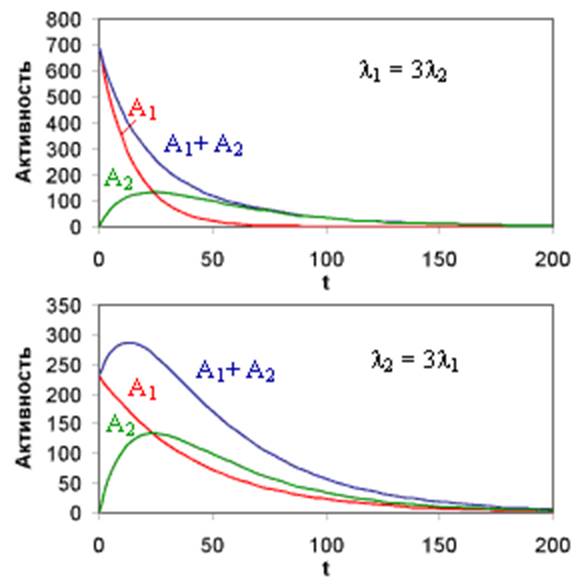
Если λ₂ < λ₁ ( T_1/2² > T_1/2¹), суммарная активность N₁(t)λ₁ + N₂(t)λ₂ будет монотонно уменьшаться.

Если λ₂ >λ₁ (T_1/2² < T_1/2¹ ), суммарная активность вначале растет за счет накопления ядер 2.

Если λ₂ >>λ₁, при достаточно больших временах вклад второй экспоненты в становится пренебрежимо мал, по сравнению со вкладом первой и, следовательно, активности второго A₂ = λ₂N₂ и первого изотопов A₁ = λ₁N₁ практически сравняются. В дальнейшем активности как первого, так и второго изотопов будут изменяться во времени одинаково

A₁(t) = N₁₀λ₁= N₁(t)λ₁ = A₂(t) = N₂(t)λ₂.

То есть устанавливается так называемое вековое равновесие, при котором число ядер изотопов в цепочке распадов связано с постоянными распада (периодами полураспада) простым соотношением.

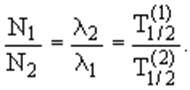
Поэтому в естественном состоянии все изотопы, генетически связанные в радиоактивных рядах, обычно находятся в определенных количественных соотношениях, зависящих от их периодов полураспада.

⇐ Предыдущая 12