
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
РЕШЕНИЕ ЗАДАЧ
РЕШЕНИЕ ЗАДАЧ
КЛЮЧЕВЫЕ ЗАДАЧИ
1.Точка С – середина отрезка AB, а О – произвольная точка на плоскости (рис. 6). Доказать, что 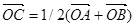 .
.
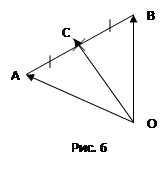 Доказательство:
Доказательство:
По правилу треугольника 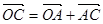 ,
, 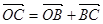 . Складывая эти равенства, получаем:
. Складывая эти равенства, получаем:
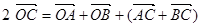 .
.
Так как точка С – середина отрезка АВ, то 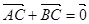 . Таким образом,
. Таким образом, 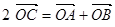 , или
, или 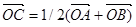 .
.
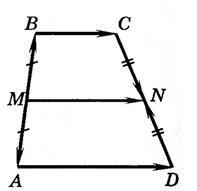
2.Доказать, что средняя линия трапеции параллельна основаниям и длина ее равна полусумме длин оснований.
 Дано:
Дано:
ABCD– трапеция
M– середина AВ
N– середина СD
|
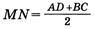
Анализ. Для доказательства параллельности достаточно показать, что векторы 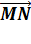 и
и  коллинеарны
коллинеарны
Решение.
1) Согласно рассмотренной задаче 1 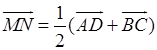 .
.
2) Так как 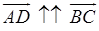 , то
, то 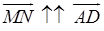 и, значит, MN || AD.
и, значит, MN || AD.
3) Так как 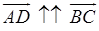 , то
, то 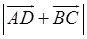 = AD + BC, поэтому
= AD + BC, поэтому
MN = 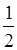 (AD + BC).
(AD + BC).
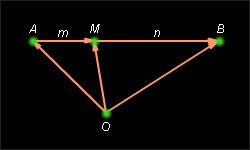
3. Разделить данный отрезок AB в данном отношении m : n, то есть найти точку M принадлежит AB, такую, что AM : MB = m : n.
|
| Рис.3 |
Решение:
Очевидно, что M принадлежит AB делит отрезок AB в заданном отношении m : n тогда и только тогда, когда 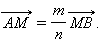 Кроме того,
Кроме того,
 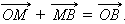
|
Отсюда
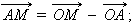 
|
Подставляя в исходное соотношение, имеем
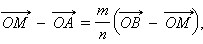
|
откуда находим
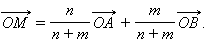
|
В частности, если M – середина отрезка AB, то m = n, и получим
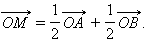
|
Если точки A и B заданы своими координатами в некоторой декартовой системе координат  то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам
то, используя формулу, можно легко найти координаты точки M в той же системе координат. Векторное равенство равносильно числовым равенствам
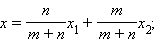 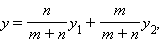
|
где 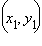 и
и 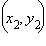 – координаты концов отрезка AB, а x и y – координаты искомой точки M.
– координаты концов отрезка AB, а x и y – координаты искомой точки M.
В частности, когда точка M является серединой отрезка AB, получаем
 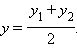
|
Таким образом, мы векторным путем получили результаты.
ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
4. Дан произвольный треугольник 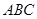 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника
. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника 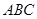 .
.
Решение
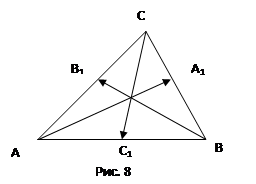 Пусть
Пусть  ,
, 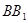 ,
, 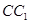 - медианы треугольника
- медианы треугольника 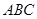 (рис.8). Тогда
(рис.8). Тогда 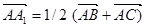 ,
, 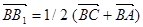 ,
, 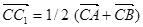 . Сложив эти равенства, получим
. Сложив эти равенства, получим
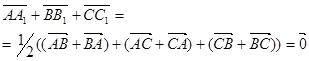
Отсюда следует, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника 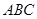 .
.
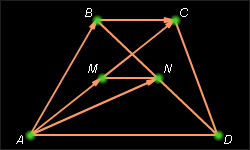
5. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям.
|
| Рисунок 11 |
Пусть M и N – середины диагоналей трапеции ABCD (см. рис. 11). Покажем, что MN || AD. Для этого достаточно показать, что 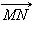 коллинеарен
коллинеарен 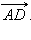
Так как M и N – середины отрезков AC и BD, то
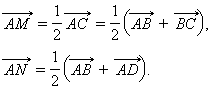
|
Следовательно,
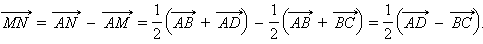
|
Но  коллинеарен вектору
коллинеарен вектору 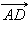 , поэтому
, поэтому 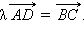 Тогда
Тогда

|
то есть 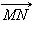 коллинеарен
коллинеарен 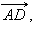 что и требовалось доказать.
что и требовалось доказать.
ЗАДАЧИ НА САМОСТОЯТЕЛЬНУЮ РАБОТУ
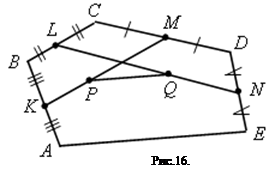 6. Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.
6. Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.
Дано:
ABCDЕ– пятиугольник
K, L, M, N – середины сторон AB, BC, CD, DE
P и Q – середины отрезков KM и LN
Доказать PQ || AE и PQ = 1/4 AE.
Решение.
Пусть О – произвольная точка. Согласно соотношению 3
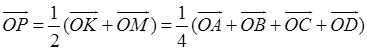 .
.
Аналогично,
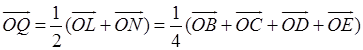 .
.
Из этих равенств следует, что
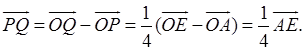
Отсюда следует, что PQ || AE и PQ = 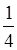 AE.
AE.
7. В параллелограмме  дано:
дано: 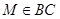 и
и 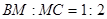 ;
; 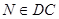 ,
, 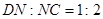 ;
; 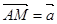 ,
, 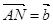 . Выразить векторы
. Выразить векторы 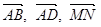 и
и 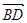 через
через 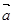 и
и 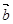 .
.
Решение
Пусть  - параллелограмм (рис. 12), в котором
- параллелограмм (рис. 12), в котором 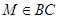 ,
,  ,
,  ,
,  ,
, 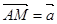 ,
, 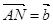 .
.
Выразим  через
через 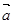 и
и 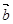 .
. 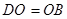 ,
, 
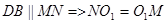 .
.
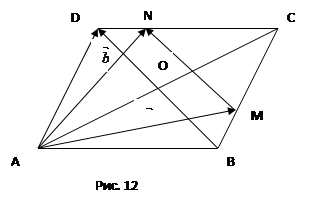 Тогда
Тогда 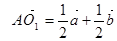 .
.
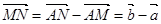 ,
,
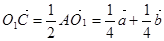 ,
,
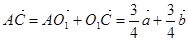 .
.
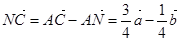 ,
,
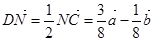 ,
,
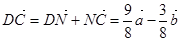 ,
, 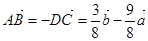 ,
,
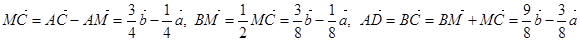

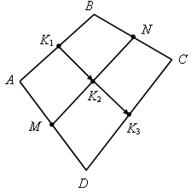
8. Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM:MD=BN:NC== 3:4.
Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.
Доказательство. Пусть K1 – середина AB, K2 – середина MN, K3 – середина CD. Согласно соотношению 8 имеем
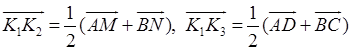 .
.
Из условия следует, что 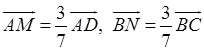 ,
,
поэтому 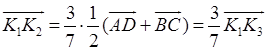 .
.
Таким образом, векторы 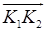 и
и 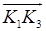 коллинеарны, и, значит, точки K1, K2 и K3 лежат на одной прямой.
коллинеарны, и, значит, точки K1, K2 и K3 лежат на одной прямой.
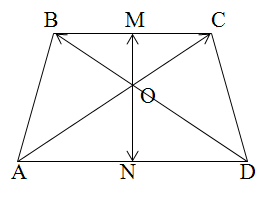 9. В трапеции ABCD точки M и N середины оснований BC и AD соответственно. Докажите, что точка О пересечения диагоналей AC и BD лежит на прямой MN.
9. В трапеции ABCD точки M и N середины оснований BC и AD соответственно. Докажите, что точка О пересечения диагоналей AC и BD лежит на прямой MN.
Доказательство.
|
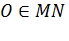 достаточно доказать, что
достаточно доказать, что 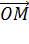 и
и 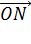 коллинеарны.
коллинеарны.
Для этого нужно разложить векторы 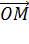 и
и 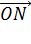 по базисным векторам.
по базисным векторам.
В качестве базисных векторов возьмём 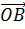 =
= 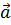
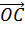 =
= 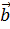 . По соотношению 3
. По соотношению 3
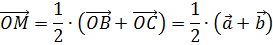
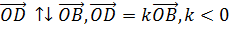

Из подобия треугольников BOC и AOD: 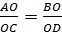
Значит k=n, т.е. 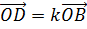 ,
,  ,
,
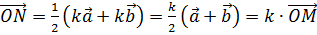 , значит
, значит 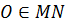 .
.
10. На катетах прямоугольного треугольника АВС с прямым углом С построены квадраты АСQP и BCRS. Точка М- середина гипотенузы АВ. Доказать, что отрезки СМ и QR перпендикулярны.
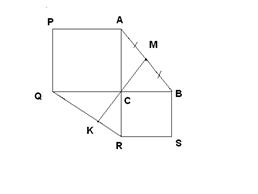
Решение.
1). Так как М- середина АВ, то СМ= ½ ∙(СА+СВ).
2). QR=CR-CQ.
3). QR∙CM=½(CA+CB)∙ (CR-CQ)= ½∙(CA∙ CR-CA ∙CQ+CB∙ CR-CB∙CQ).
Так как CA и CQ перпендикулярны, то CA∙CQ=0; аналогично CB ∙CR=0.
Учитывая это, получим: QR∙ CM= ½(CA∙ CR-CB∙ CQ)=
= ½∙(CA∙ CR ∙cos180° – CB∙ CQ ∙cos180°)=½∙ (-CA∙ CR+CB∙ CQ).
А так как CR=CB и CQ=CA, то QR ∙CM= ½∙(CB∙ CA-CA∙ CB)=0.
4). Итак, QR∙ CM=0, поэтому отрезки QR и CM перпендикулярны.
Что и требовалось доказать.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|