
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ВЕКТОРНЫЙ МЕТОД
ВЕКТОРНЫЙ МЕТОД
При решении геометрических задач векторным методом нужно от геометрической постановки задачи перейти к ее векторному описанию. Затем, пользуясь свойствами векторов и операциями над ними, найти некоторое векторное соотношение, отражающее данные и условие задачи, из которых можно получить решение задачи. Рассмотрим несколько примеров.
КЛЮЧЕВЫЕ ЗАДАЧИ
1. Точка С – середина отрезка AB, а О – произвольная точка на плоскости (рис. 6). Доказать, что 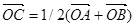 .
.
2.Доказать, что средняя линия трапеции параллельна основаниям и длина ее равна полусумме длин оснований.
3. Разделить данный отрезок AB в данном отношении m : n, то есть найти точку M принадлежит AB, такую, что AM : MB = m : n.
ЭЛЕМЕНТАРНЫЕ ЗАДАЧИ
4 Дан произвольный треугольник 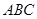 . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника
. Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника 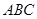 .
.
5. Докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям.
ЗАДАЧИ НА САМОСТОЯТЕЛЬНУЮ РАБОТУ
6. Точки K, L, M, N – середины сторон AB, BC, CD, DE пятиугольника ABCDE, а точки P и Q – середины отрезков KM и LN. Докажите, что PQ || AE и PQ = 1/4 AE.
7.В параллелограмме 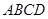 дано:
дано: 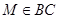 и
и 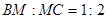 ;
; 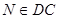 ,
, 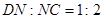 ;
;  ,
,  . Выразить векторы
. Выразить векторы 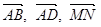 и
и 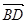 через
через 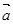 и
и 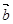 .
.
8. Точки M и N лежат соответственно на сторонах AD и BC четырехугольника ABCD, причем AM:MD=BN:NC== 3:4.
Докажите, что середины отрезков AB, MN и CD лежат на одной прямой.
9. В трапеции ABCD точки M и N середины оснований BC и AD соответственно. Докажите, что точка О пересечения диагоналей AC и BD лежит на прямой MN.
10. На катетах прямоугольного треугольника АВС с прямым углом С построены квадраты АСQP и BCRS. Точка М- середина гипотенузы АВ. Доказать, что отрезки СМ и QR перпендикулярны.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|