по дисциплине Оптимальные и адаптивные системы

по дисциплине "Оптимальные и адаптивные системы"

1. Теоретический вопрос – один из 15.

2. Составить уравнение Эйлера для функционала: .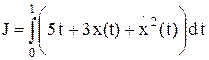

Найти экстремаль, проходящую через точки х(0) = 0, х(1) = 1.

3. Составить уравнение Эйлера – Пуассона для функционала: .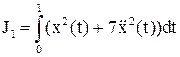

4. Записать функции Лагранжа и Гамильтона для задачи оптимального управления объектом 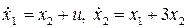с функционалом качества .

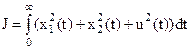5. С использованием метода динамического программирования записать уравнение в частных производных для определения функции Беллмана S(x) (уравнение Гамильтона-Якоби-Беллмана) в задаче оптимального управления п.5.

Билет рассмотрен и утвержден на заседании кафедры '' " 2013г.

Заведующий кафедрой .

⇐ Предыдущая 12