
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Линейные неравенства и их системы.
Линейные неравенства и их системы.
В целом линейные неравенства решаются аналогично тому, как решаются линейные уравнения, однако существуют и различия:
1) если при неизвестном х стоит отрицательный коэффициент, то при переносе его в другую часть неравенства знак неравенства нужно поменять на противоположный (см. теорему 3);
2) решением неравенства обычно является не одно число, а числовой промежуток;
3) Для решения системы, состоящей из двух линейных неравенств, следует:
а) решить каждое неравенство в отдельности;
б) обозначить множество решений каждого из неравенств на координатной прямой;
в) в ответ записать их пересечение.
Пр: -3(х + 2) ≤ 6х, х + 2 ≥ -2х, х + 2х ≥ -2, 3х ≥ -2, х ≥ 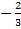 . Ответ: х
. Ответ: х 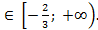
Практическая часть
1. Сократите дробь: а)  ; б)
; б) 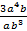 ; в)
; в) 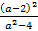 .
.
2. Выполните сложение и вычитание дробей: а) 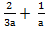 ; б)
; б) 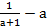 ; в)
; в)  .
.
3. Выполните умножение и деление дробей: а) 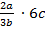 ; б)
; б) 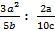 .
.
4. Выполните действия:
а) Прибавьте к обеим частям неравенства 2а + 3b > а – 2b одно и то же число: а) -3; б) 2b.
б) Умножьте обе части неравенства 4а > 3 на одно и тоже число: а)  ; б) -3.
; б) -3.
в) Разделите обе части неравенства -25х < -30 на одно и тоже число: а) 2; б) -5.
5. Пусть а < b. Сравните : а) - 4,2а и - 4,2b; б)  и
и  ; в)
; в)  и
и  ;
;
6. Выполните: а) сложение неравенств: а) 5 > - 8 и 8 > 5; б) 3х + у < 2х + 1 и 3у – 2х < 14 – 2а.
б) умножение неравенств: а) 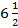 <
< 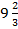 и 4 < 6; б) х – 2 > 1 и 5 > х +3.
и 4 < 6; б) х – 2 > 1 и 5 > х +3.
7.На координатной прямой отмечены числа a и b. В ответе укажите номер правильного варианта.
 Какое из следующих утверждений является верным?
Какое из следующих утверждений является верным?
1)  ; 2)
; 2)  ; 3)
; 3) 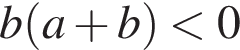 ; 4)
; 4) 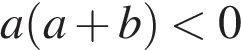 .
.
8. С помощью графика функции найти, при каких значениях х значения функции положительны, отрицательны, больше 1, меньше 1: а ) у = 2х +4; б) у = - 3х +6.
9. Решить неравенства: а) х + 2 ≥ 15; б) х – 6 < 8 ; в) - 4 > 5 – у ; г) 2х + 4 ≤ 0 ; д) 3(х – 2) + х < 4х + 1;
е) 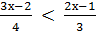 ; ж)
; ж) 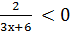 ; з) При каких значениях a выражение 5a + 9 принимает отрицательные значения? 1)
; з) При каких значениях a выражение 5a + 9 принимает отрицательные значения? 1)  ; 2)
; 2)  ; 3)
; 3) 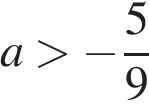 ; 4)
; 4) 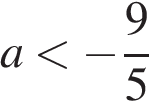
10. Решите системы неравенств:
а)  На каком рисунке изображено множество её решений?
На каком рисунке изображено множество её решений? 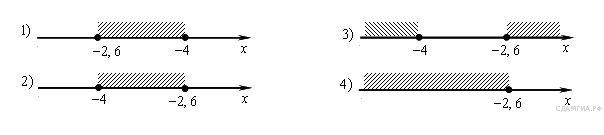
б)  На каком рисунке изображено множество её решений?
На каком рисунке изображено множество её решений?

11. Сколько железнодорожных платформ потребуется для перевозки 183 контейнеров, если на одной платформе можно разместить не более 5 контейнеров.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|