Образовательный минимум по алгебре за I четверть.

Стр 1 из 2Следующая ⇒

Образовательный минимум по алгебре за I четверть.

Теоретическая часть

Алгебраические дроби

Основное свойство дроби

Основное свойство дроби:

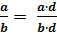, где b, d ≠ 0.

Сокращение

Приведение к общему знаменателю

Сравнение

Сложение (вычитание)

Сложение (вычитание)	Умножение	Деление	Степень
			,

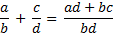
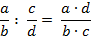
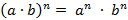
Неравенства

Основные свойства чисел	Основные свойства числовых неравенств
	Теорема 1.Если а > b и b > c, то а > с.
	Теорема 2.Если к обеим частям неравенства прибавить одно и то же число, то знак неравенства не изменится. Пр. если а > b, то а – 5 > b – 5.
	Теорема 3.Если обе части неравенства умножить на одно и то же положительное число, то знак неравенства не изменится. Если обе части неравенства умножить на одно и то же отрицательное число, то знак неравенства изменится на противоположный. Пр. если а > b, то 5∙a > 5∙b; если а > b, то -5∙a < - 5∙b.
	Теорема 4.При сложении неравенства одинакового знака получается неравенства того же знака: еслиа > bис > d,тоа + c > b + d.
	Теорема 5.При умножении неравенства одинакового знака, у которых левые и правые части положительны, получается неравенство того же знака: еслиа >b и с > d (a, b, c, d положительные числа),то ас > bd.

Решение неравенств

Решить неравенство означает найти все его значения или установить, что их нет.

12 Следующая ⇒