
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Прямая призма.. Определение.. Правильная призма.. П араллелепипед.
Прямая призма.
Определение.

Призма называется прямой, если все её боковые грани являются прямоугольниками.
! Высота прямой призмы равна ее боковому ребру.
Для прямой призмы, у которой боковые ребра перпендикулярны плоскостям оснований, площадь боковой поверхности вычисляется по формуле: 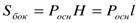 .
.
Правильная призма.
Определение: Призма называется правильной, если основаниями её служат правильные многоугольники и боковые рёбра перпендикулярны к основаниям.;
В зависимости от числа углов в основании призма называется треугольной, четырёхугольной, пятиугольной и т. д.
Боковыми гранями любой правильной призмы служат прямоугольники.
П араллелепипед.
Определение.
Параллелепипед— призма, основаниями которой являются параллелограммы.
Типы параллелепипеда:
Прямоугольный параллелепипед - это параллелепипед, у которого все грани прямоугольники;
Прямой параллелепипед - это параллелепипед, у которого 4 боковые грани прямоугольники;
Куб - это прямоугольный параллелепипед с равными измерениями. Все шесть граней куба - равные квадраты.
Основные элементы:
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх ребер прямоугольного параллелепипеда, имеющих общий конец, называют его измерениями.
Свойства:
· Параллелепипед симметричен относительно середины его диагонали.
· Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
· Противолежащие грани параллелепипеда параллельны и равны.
· Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы:
Прямой параллелепипед
Площадь боковой поверхности 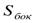 =Ро*h, где Ро - периметр основания, h - высота
=Ро*h, где Ро - периметр основания, h - высота
Площадь полной поверхности 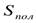 =Sб+2Sо, где Sо - площадь основания
=Sб+2Sо, где Sо - площадь основания
Прямоугольный параллелепипед
Площадь боковой поверхности 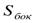 =2c(a+b),где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда
=2c(a+b),где a, b - стороны основания, c - боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности  =2(ab+bc+ac)
=2(ab+bc+ac)
Куб
Площадь боковой поверхности 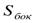 =4
=4  , где а - ребро куба
, где а - ребро куба
Площадь полной поверхности  =6
=6  , где а - ребро куба
, где а - ребро куба
Домашнее задание: Погорелов А.В.«Геометрия 10 - 11», §5 №26.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|