Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Определение.

Определение.

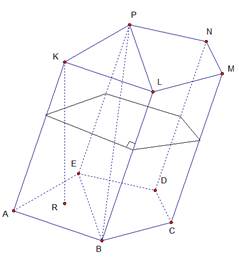
Многогранник, составленный из двух равных многоугольников А₁А₂...А_n и B₁B₂...B_n, расположенных в параллельных плоскостях, и n-параллелограммов, называется призмой.

Многоугольники А₁А₂...А_n и B₁B₂...B_n называются основаниями, а параллелограммы - боковыми гранями призмы. Отрезки А₁B₁, А₂B₂, ... , А_nB_n называются боковыми рёбрами призмы. Боковые рёбра призмы равны друг другу как отрезки параллельных прямых, заключённые между параллельными плоскостями. Призму с основаниями А₁А₂...А_n и B₁B₂...B_n обозначают А₁А₂...А_nB₁B₂...B_n и называют n-угольной призмой.
Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.
Если боковые рёбра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае - наклонной. Высота прямой призмы равна ее боковому ребру.

Площадью полной поверхности призмы называется сумма площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней.

S_полн = S_бок + 2S_осн

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Элементы призмы

Название	Определение	Обозначения на чертеже	Чертеж
Основания	Две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях.	ABCDE, KLMNP
Боковые грани	Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом.	ABLK, BCML, CDNM, DEPN, EAKP
Боковая поверхность	Сумма площадей боковых граней.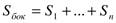
Полная поверхность	Сумма площадей двух оснований и боковой поверхности.	Sпол= =Sбок+2Sосн
Боковые ребра	Общие стороны боковых граней. Боковые ребра призмы параллельны и равны.	AK, BL, CM, DN, EP
Высота	Перпендикуляр, проведенный из какой – нибудь точки одного основания к плоскости другого основания.	KR
Диагональ призмы	Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.	BP
Диагональная плоскость	Плоскость, проходящая через боковое ребро призмы и диагональ основания.
Диагональное сечение	Пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе его частные случаи — ромб, прямоугольник, квадрат.	EBLP
Перпендикулярное сечение	Пересечение призмы и плоскости, перпендикулярной ее боковому ребру. · Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы. · Перпендикулярное сечение перпендикулярно ко всем боковым граням