Пример 8.Найти координаты точки m, изображающей комплексное число .

⇐ ПредыдущаяСтр 2 из 2

Пример 8.Найти координаты точки m, изображающей комплексное число .

Решение.

Выделим действительную и мнимую часть этого числа:

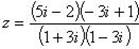
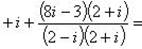
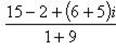
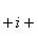
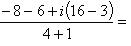
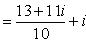
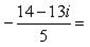
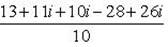
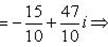
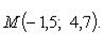
Пример 9.Найти все значения корней:

а) ;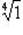

б) .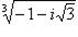

Решение.

а) Запишем комплексное число 1 в тригонометрической форме

1 = cos 0° + i sin 0°; затем по формуле Муавра, находим

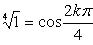
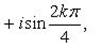
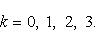
Следовательно,

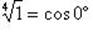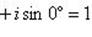
	при k = 0;
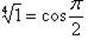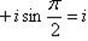
	при k = 1
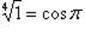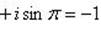
	при k = 2;
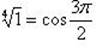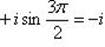
	при k = 3.

б) Записав комплексное число 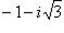в тригонометрической форме

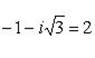
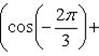
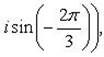
находим

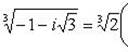
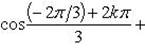
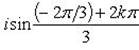
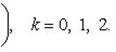
Отсюда

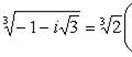
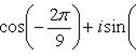
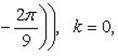
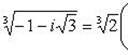
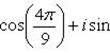
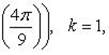
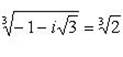
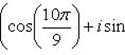
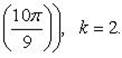
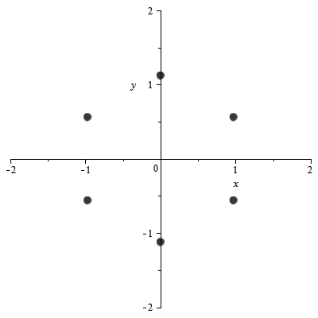
Пример 10.Изобразить корни 6 степени из 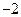на комплексной плоскости.

Решение.

Представим число 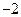как комплексное в алгебраической форме записи, т.е. в виде 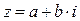. Получим 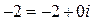. Таким образом 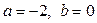. После чего переведем его в тригонометрическую форму: 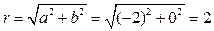, , 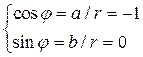т. е. 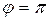. Тогда 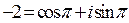. Используем формулу для корней 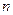степени из комплексного числа 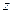в тригонометрической форм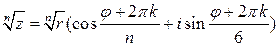е: , где 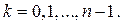Получаем 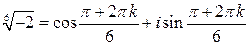, где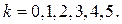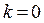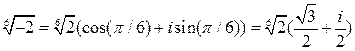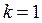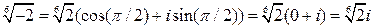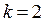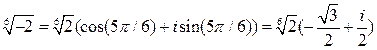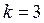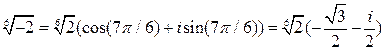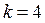

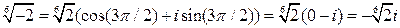При : .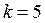

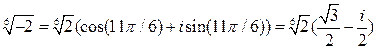Пример 11.Решить уравнение: z⁶ + 1 = 0.

Решение.

Имеем 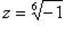. Для вычисления всех значений 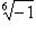применим формулу Муавра:

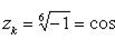
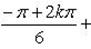
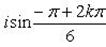
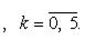
Отсюда

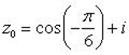
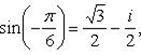
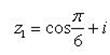
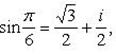
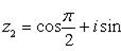
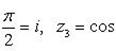
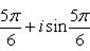
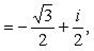
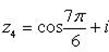
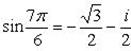
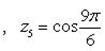
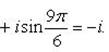
Пример 12. Доказать, что

Решение.

Левую часть разложим по формуле суммы кубов двух чисел:

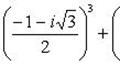
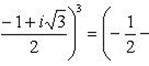
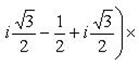
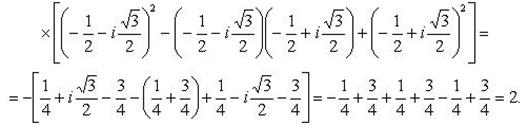
Пример 13.Найти число, сопряженное с числом

Решение.

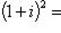
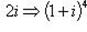
Заметим, что 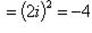. Тогда

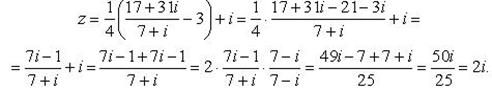
Тогда сопряженное число .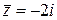

Пример 14.Установить, при каких действительных значениях x и y являются противоположными следующие комплексные числа: и .

Решение.

Приведем числа z₁ и z₂ к алгебраической форме записи:

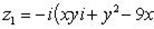
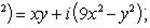
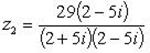
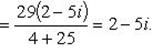
Согласно условию задачи, получаем систему:

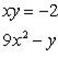
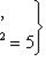(1)

Умножим обе части первого уравнения на 5, а второго - на 2 и сложим получившиеся при этом результаты:

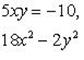
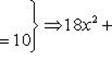
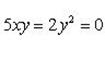- однородное уравнение.

Разделим обе его части на y², получим: 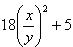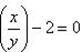- квадратное уравнение относительно 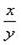. Решив его, получим 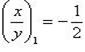и 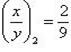, т. е. y = -2x или 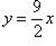. Подставим эти значения, например, в первое уравнение из (1), получим .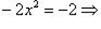

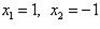Тогда y₁ = -2, y₂ = 2.

Аналогично, при 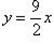получаем 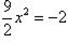- это уравнение действительных решений не имеет.

Ответ: {(1; -2), (-1; 2)}.

⇐ Предыдущая 12