СЕМИНАР 1. Комплексные числа

СЕМИНАР 1

Комплексные числа

Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:

1) два комплексных числа z₁ = (x₁, y₁) и z₂ = (x₂, y₂) называются равными, если x₁ = x₂ и y₁ = y₂;

2) суммой комплексных чисел z₁ и z₂ называется комплексное число z вида z = (x₁ + x₂, y₁ + y₂);

3) разностью комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ + z = z₁, откуда находим z = z₁ - z₂ = (x₁ - x₂, y₁ - y₂).

4) произведением комплексных чисел z₁ и z₂ называется комплексное число z = (x₁x₂ - y₁y₂, x₁y₂ + x₂y₁);

5) частным комплексных чисел z₁ и z₂ называется комплексное число z такое, что z₂ · z = z₁. Отсюда находим

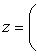
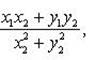
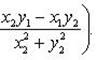
4) множество комплексных чисел (x;0), xϵR, отождествляется с множеством действительных чисел R.

Комплексное число (0;1) обозначается символом i = (0;1). Тогда 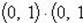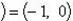, т. е. i² = -1. Произвольное комплексное число z можно записать в виде

z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1) · (y, 0) = x + iy.

Эта запись называется алгебраической формой комплексного числа. Комплексное число 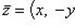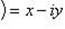называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy.

Пример 1. Доказать, что:

а) ;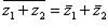

б) ;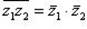

в) .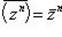

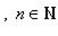Решение.

Пусть z₁ = (x₁, y₁), z₂ = (x₂, y₂).

а) По определению сопряженного числа

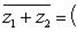
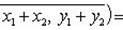
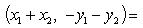
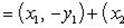
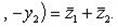
б) Имеем

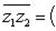
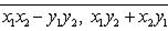
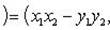
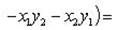
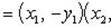
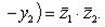
в) Запишем комплексное число z в тригонометрической форме

z = (r cos θ, r sin θ), тогда

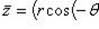
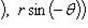Пользуясь формулой Муавра, имеем

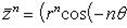
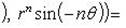
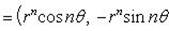
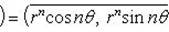
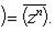
Пример 2. Выполнить указанные операции:

а) (2 - i)(2 + i)² - (3 - 2i) + 7;

б) (1 + i)⁴;

в) .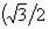

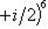Решение.

С комплексными числами, записанными в алгебраической форме, операции сложения, вычитания и умножения можно производить так же, как с действительными биномами. При этом пользуемся тем, что i² = -1, i³ = i² i = -i, i⁴ = i³ i = -i² = 1, и т. д.

а) Имеем

(2 - i)(2 + i)² = - (3 - 2i) + 7 = (2 - i)(2 + i)² + 4 + 2i =

= (2 + i)((2 - i)(2 + i) + 2) = (2 + i)(4 + 1 + 2) = 14 + 7i.

б) Согласно формуле бинома Ньютона,

(1 + i)⁴ = 1 + 4i + 6i² + 4i³ + i⁴ = 1 + 4i - 6 - 4i + 1 = -4.

в) .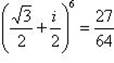

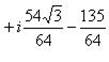
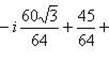
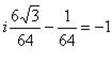Пример 3.Делится ли многочлен x⁴ + 2x² + 4(1 + i) на x - 1 + i?

Решение.

Если данный многочлен делится на x - (1 - i), то комплексное число 1 - i должно быть его корнем. Подставим это число в многочлен, получим (1 - i)⁴ + 2(1 - i)² + 4(1 + i) = - 4 + 2(-2i) + 4 + 4i = 0. Следовательно данный многочлен делится на x - 1 + i.

Пример 4.Найти частное комплексных чисел:

а) ;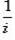

б) ;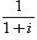

в) .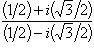

Решение.

Формулу для нахождения частного комплексных чисел z₁ и z₂ запишем в виде

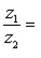
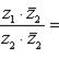
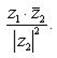
Пользуясь этой формулой, находим

а) ;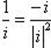

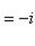б) ;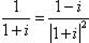

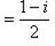
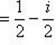в) .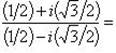

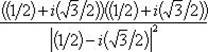
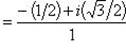
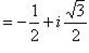Пример 5.Даны комплексные числа z₁ = -2 + 5i и z₂ = 3 - 4i. Найти:

а) z₁ + z₂;

б) z₂ - z₁;

в) z₁z₂;

г) z₁/z₂.

Решение.

а), б). Для комплексных чисел z₁ = x₁ + iy₁, z₂ = x₂ + iy₂ сумма и разность находятся по формулам z₁ ± z₂ = (x₁ ± x₂) + i(y₁ ± y₂).

В нашем случае имеем z₁ + z₂ = (-2 + 3) + i(5 - 4) = 1 + i, z₂ - z₁ = 3 - (-2) + i(-4 - 5) = 5 - 9i.

в) Перемножаем z₁ и z₂ как двучлены с учетом равенства i² = -1:

z₁z₂ = (-2 + 5i)(3 - 4i) = (-2)3 + 15i + 8i - 20i² = -6 + 20 + i(15 + 8) = 14 + 23i.

г) Для нахождения частного 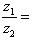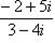умножим числитель и знаменатель этой дроби на число, сопряженное знаменателю, т.е. на 3 + 4i; получим

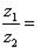
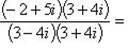
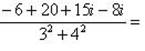
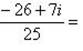
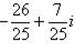Пример 6.Представить следующие комплексные числа в тригонометрической форме:

а) - 3;

б) - i;

в) 1 + i;

г) .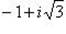

Решение.

Имеем

а) | -3 | = 3, θ = π, -3 = 3(cos π + i sin π);

б) | -i | = 1, θ = -π/2, -i = cos(-π/2) + i sin(-π/2);

в) ;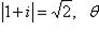

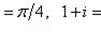
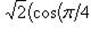
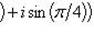г) .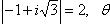

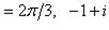
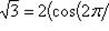
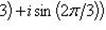Пример 7.Установить, при каких действительных значениях x и y равны следующие комплексные числа:z₁ = x² = xyi - 5 + i и z₂ = xi - y² + yi.

Решение.

Согласно равенству комплексных чисел, получаем следующую систему уравнений:

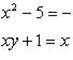
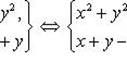
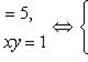
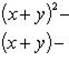
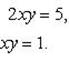(1)

Умножаем обе части второго уравнения на 2 и вычтем результат из первого уравнения, получим (x + y)² - 2(x + y) - 3 = 0 - квадратное уравнение относительно x + y. Решив его, получим x + y = 3 или x + y = -1.

Таким образом, система (1) распадается на две системы

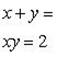
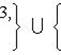
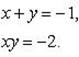
Их решениями являются: x₁ = 1, y₁ = 2; x₂ = 2, y₂ = 1 и x₃ = 1, y₃ = -2, x₄ = -2, y₄ = 1.

12 Следующая ⇒