Определители.. Практика 2.. Решение.. Решение.. Решение.. Решение.

2. Определители.

Задача 13. = .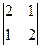

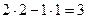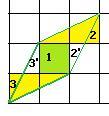
Для параллелограмма, построенного на базе системы векторов (2,1) и (1,2), площадь равна 3. Если область 2’ перенести в область 2, то видно, что получается половина прямоугольника площади 2 (выделено жёлтым). То есть площадь равна 1. Аналогично 3’ в 3. Там тоже площадь 1. Кроме того, в центре квадрат площади 1.

Практика 2.

Задача 14. Найти определитель .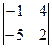

Решение. = .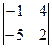

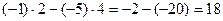Ответ. 18.

Задача 15. Найти определитель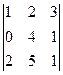

Решение.Допишем копии первых двух столбцов, проведём 3 параллельных линии (главная диагональ и ещё две). Перемножим все эти тройки элементов и внесём в общую сумму с их исходным знаком. А вот для побочной диагонали и линий, ей параллельных, со сменой знака.

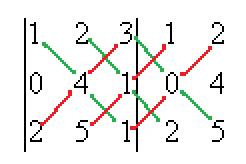
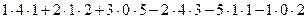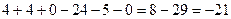Ответ. .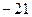

Задача 16. Найти определитель .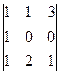

Решение.

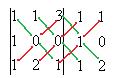
То, что перемножено по зелёным линиям, включим в сумму со знаком плюс, а по красным - со знаком минус.

= .

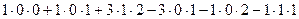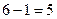Ответ. 5.

Задача 17. Найти определитель .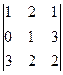

Решение.

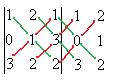
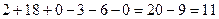. Ответ. 11.

Задача 18. Найти определитель .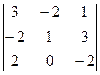

Решение.

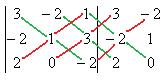
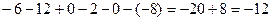. Ответ. .

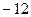Задача 19. Найти определитель .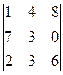

Решение.

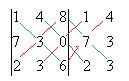
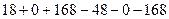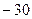= . Ответ. .

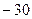Задача Дом-1.Вычислить определитель 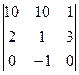. Ответ.28.

Задача 20.Вычислить определитель .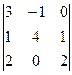

Решение.Заметим, что 1-й и 3-й столбец содержат очень похожие группы элементов а именно 1 и 2. Вычтем из 1-го столбца 3-й, а затем разложим по 1-му столбцу.

= = =

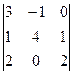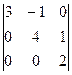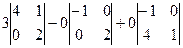Ответ.24.

Задача дом-2.Вычислить определитель 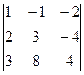. Ответ.50.

⇐ Предыдущая 12