
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Томский государственный университет систем управления и радиоэлектроники
Томский государственный университет систем управления и радиоэлектроники
Приходовский М.А.
Математика
Курс практических занятий
Семестр 1
Группы 520, 530
Томск
ТУСУР
1. Действия над матрицами.
Задача 1. Найти сумму и разность матриц: 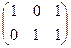 +
+ 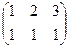
Решение.Складываем поэлементно:
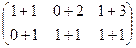 =
= 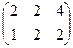 .
.
Вычитаем:
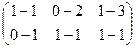 =
= 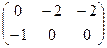 .
.
Ответ.Сумма: 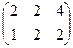 разность:
разность: 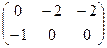 .
.
Задача 2. Найти сумму матриц: 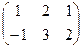 +
+ 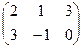
Решение.Складываем поэлементно:
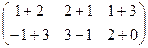 =
= 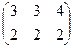 .
.
Ответ. 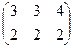 .
.
Задача 3.Даны матрицы 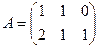 ,
, 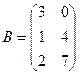 .
.
Найти 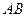 и
и 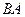 .
.
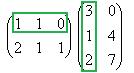
Решение.Запишем эти матрицы. Если первую разбить на строки, а вторую на столбцы, то видно, что есть всего 4 варианта скалярно умножить друг на друга вектор-строку их первой на вектор-столбец из второй.
| 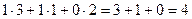
|
| 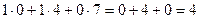
|
| 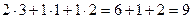
|
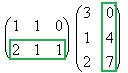
| 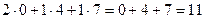
|
Например, если умножаем строку номер 1 на столбец номер 2, то и число, которое при этом получается, ставим в 1 строку 2 столбец новой матрицы. Итак,
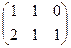
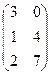 =
= 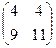 .
.
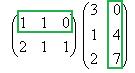
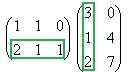
Теперь найдём 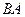 . В данном случае первую матрицу можно разрезать на 3 строки, а вторую на 3 столбца. Таким образом, получаем 9 чисел.
. В данном случае первую матрицу можно разрезать на 3 строки, а вторую на 3 столбца. Таким образом, получаем 9 чисел.
Покажем, например, как 1-я строка скалярно умножается на 1-й столбец, они обведены. 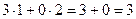 .
.
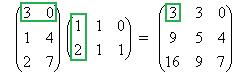
Ответ. 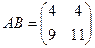
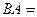
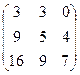 .
.
Задача 4. Найти произведение матриц:
а) 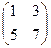
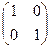 , б)
, б) 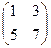
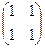 , в)
, в) 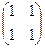
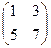 .
.
Решение.
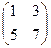
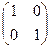 =
= 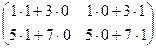 =
= 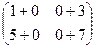 =
= 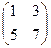 .
.
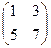
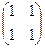 =
= 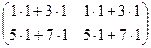 =
= 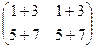 =
= 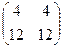 .
.
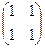
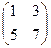 =
= 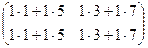 =
= 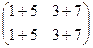 =
= 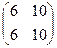 .
.
Ответ. 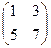 ,
, 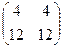 ,
, 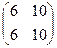 .
.
Примечания.
1) Видим, что в общем случае может не выполняться закон коммутативности при умножении матриц, то есть 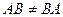
2) При умножении на матрицу, состоящую из всех единиц, исходная не получается, а вот если единицы по диагонали - получается. Матрица 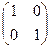 называется единичной матрицей. При этом выполняется
называется единичной матрицей. При этом выполняется 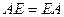 .
.
Задача 5. Дана матрица 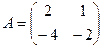 найти
найти 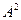 .
.
Решение. Умножим матрицу саму на себя, то есть две её копии напишем рядом и умножим их.
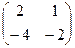
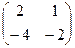 =
= 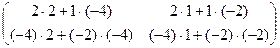 =
=
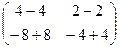 =
= 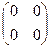 . Ответ.
. Ответ. 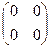 .
.
Как видно из этого примера, для матриц, в отличие от чисел, возможно, что получается нулевой объект в ответе, притом что в исходной матрице вообще ни одного нуля не было. Это из-за особенностей её строения: правый столбец в 2 раза меньше, чем левый, а нижняя строка в минус 2 раза больше, чем верхняя. И вообще, если взять пару матриц, где у первой будет пропорциональность строк (в k раз больше) а у второй - столбцов (в минус k раз меньше) получим такой же эффект.
Задача 6. Даны матрицы 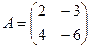
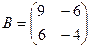 . Найти
. Найти 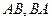 .
.
Решение. 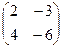
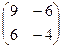 =
= 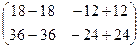 =
= 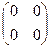 .
.
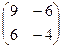
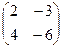 =
= 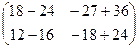 =
= 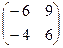 .
.
Ответ. 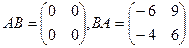 .
.
Задача 7.Найти произведение матриц 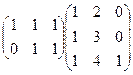 .
.
Решение. Размеры согласованы: длина строки 1-й матрицы равна высоте столбца 2-й матрицы. Первую можно мысленно разрезать на 2 строки, вторую на 3 столбца. Итого будет 6 различных произведений строк на столбцы.
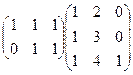 =
= 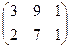 . Ответ.
. Ответ. 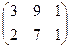 .
.
Задача 8. Вычислить 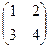
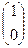 и
и 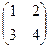
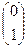 .
.
Заметим, что получаются 1-й и 2-й столбец матрицы.
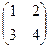
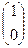 =
= 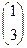 ,
, 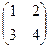
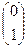 =
= 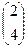 .
.
Замечание. При умножении квадратной матрицы на вектор-столбец получается снова вектор-столбец, то есть квадратная матрица фактически выступает в роли функции, отображающей векторы в пространстве (или на плоскости, если n = 2). Коротко о понятии линейного оператора и строении его матрицы и о том, что при умножении на i-й базисный вектор получается столбец номер i.
Задача 9А. Найти произведение: 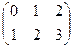
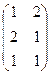 .
.
Задача 9Б. 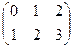
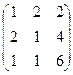 .
.
Решение.В 1-м случае размеры 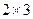 и
и 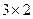 , согласованы, умножение возможно. Во 2-м случае
, согласованы, умножение возможно. Во 2-м случае 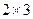 и
и 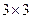 , тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.
, тоже согласованы (хоть столбцов и больше, но всё равно длина строки 1-й матрицы равна высоты столбца 2-й матрицы). Просто в ответе для 3Б получится ещё один лишний столбец справа.
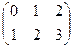
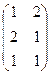 =
= 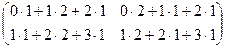 =
=
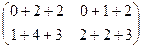 =
= 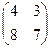 .
.
Для пункта «Б» 1-я и 2-я строка умножаются не только на 1-й и 2-й, но ещё и на 3-й столбец. Дополнительно получаем
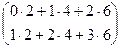 =
= 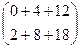 =
= 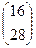 .
.
Выделим красным цветом новый столбец:
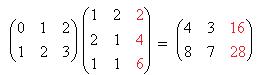
Ответ. 9А: 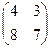 , 9Б:
, 9Б: 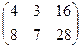 .
.
Задача 10. Даны матрицы
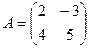 ,
, 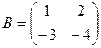 ,
, 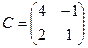 . Найти
. Найти 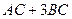 .
.
Решение. Так как матрица С находится справа во всех слагаемых, то для удобства можно использовать приведение подобных 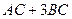 =
= 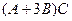 - тогда умножение надо будет проводить всего один раз, а не два.
- тогда умножение надо будет проводить всего один раз, а не два.
Сначала запишем 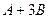 .
.
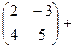
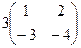 =
= 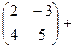
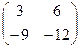 =
= 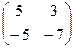 .
.
Теперь умножим на матрицу С. Точно так же, как и в прошлом примере, мысленно обведём строку из 1-й матрицы на столбец из 2-й.
Есть 4 варианта это сделать:
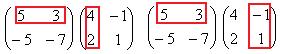
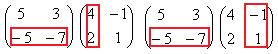
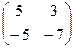
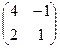 =
= 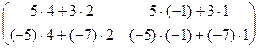 =
= 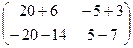 =
= 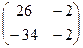 .
.
Ответ. 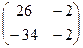 .
.
Задача домашняя 1. Найти произведение 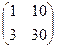
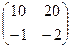 .
.
Ответ. 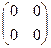 .
.
Задача дом-2. 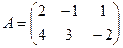
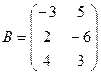 Найти
Найти 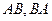 .
.
Ответ. 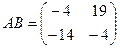 ,
, 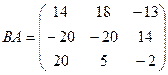 .
.
Задача дом-3. 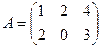
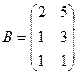 . Найти
. Найти 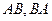 .
.
Ответ. 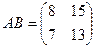 ,
, 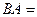
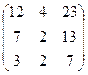 .
.
Задача 11. Дана матрица 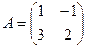 . Найти
. Найти 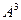 .
.
Решение. Сначала умножим две, и найдём 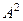 .
.
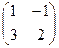
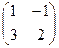 =
= 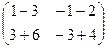 =
= 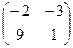 .
.
Теперь домножим ещё на одну матрицу А, чтобы найти 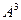 .
.
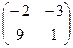
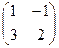 =
= 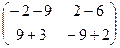 =
= 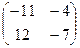 .
.
Ответ. 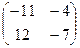 .
.
Замечание.Несмотря на то, что в общем случае коммутативности по умножению матриц нет, но если матрица 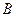 совпадает с матрицей
совпадает с матрицей 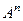 , тогда
, тогда 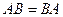 . Например, в этой задаче,
. Например, в этой задаче, 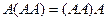 из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.
из-за ассоциативности, т.е. неважно, домножить третий раз слева или справа.
Задача дом-4. Найти 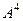 для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить
для этой же матрицы. Замечание. Здесь есть 2 метода решения: либо умножить 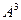 , полученную в прошлой задаче, ещё раз на
, полученную в прошлой задаче, ещё раз на 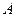 , либо взять
, либо взять 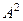 , полученную на первом этапе, и её умножить саму на себя. Ответ.
, полученную на первом этапе, и её умножить саму на себя. Ответ. 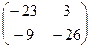 .
.
Задача 12.Найти произведение 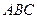 , где
, где
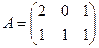 ,
, 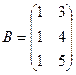 ,
, 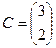 .
.
Решение.Вычислим 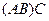 , сначала умножим первые две матрицы:
, сначала умножим первые две матрицы:
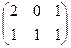
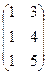 =
= 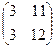 . Теперь умножим на третью матрицу.
. Теперь умножим на третью матрицу.
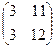
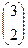 =
= 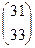 . Ответ.
. Ответ. 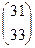 .
.
Замечание. Если вычислять 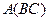 , то получается точно такой же результат, т.к. выполняется закон ассоциативности.
, то получается точно такой же результат, т.к. выполняется закон ассоциативности.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|