ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ 5 страница

Рис. 48

Эмиссия возникает в контакте металла катода с окружающим вакуумом. При косвенном накале катод нагревается с помощью расположенной внутри него нити накала до нескольких сотен градусов, а при прямом накале ток проходит через катод и разогревает его. Для улучшения эмиссионных свойств или получения необходимого тока эмиссии I_э подбирают специальный металл (иногда полупроводник) катода с минимальной работой выхода или покрывают его специальным составом.

На небольшом расстоянии от катода располагается второй электрод – анод. Если напряжение на аноде по отношению к катоду положительное, анод создаёт между катодом и анодом положительное электрическое поле. Это поле заставляет электроны двигаться от катода к аноду. Возникает анодный ток I_а. При отрицательном напряжении на аноде этого тока нет, так как эмиссия свободных электронов происходит только с катода, и конвекционный ток не протекает. Отсюда односторонняя проводимость, как и в диодах на основе m-n и p-n переходов.

В электровакуумном триоде (рис. 49) имеется ещё один электрод –

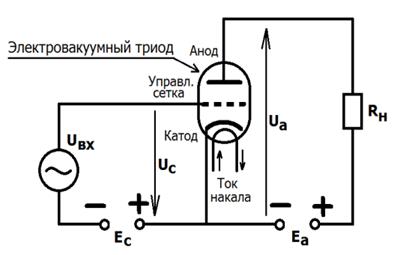
Рис. 49

управляющая сетка – сетчатый электрод, расположенный между катодом и анодом. Через просветы в сетке могут пролетать электроны. На управляющую сетку подаётся напряжение входного сигнала u_вх и постоянное напряжение смещения от источника Е_с. Суммарное напряжение на сетке u_c = u_вх + Е_с, как правило, небольшое иотрицательное. При этом электроны не перехватываются сеткой и сеточного тока нет. В противном случае, при положительном u_c, наблюдается захват сеткой части электронов из потока, идущего от катода к аноду. В результате появляется сеточный ток, растёт потребление мощности от источника сигнала, уменьшается коэффициент усиления по мощности. Уменьшается также полезный выходной ток I_а.

Расположение сетки, её «густота», величины сеточного и анодного напряжения таковы, что суммарное поле сетки и анода вблизи катода положительное и возникает значительный I_а. В то же время поле сетки сильно влияетна величину I_ат.к. она расположена намного ближе к катоду и эффективно управляет потоком электронов. В результате, из-за отсутствия или малости входного (сеточного) тока мощность источника сигнала ничтожна по сравнению с мощностью, выделяемой в нагрузке Р_н = I_а²∙ R_н. Следовательно, лампа обладает большим коффициентом усиления по мощности.

С ростом отрицательного напряжения на сетке суммарное поле у катода ослабевает. Это вызывает уменьшение тока анода I_а. При достаточно большом отрицательном напряжении на сетке u_C ток анода I_а исчезает (режим отсечки). Электрические свойства триода хорошо отражает семейство анодных характеристик – зависимостей I_аот U_a при различных напряжениях на управляющей сетке E_с. Типичное триода изображено На рис. 50 изображено семейство анодных характеристик пентода, у которого соединены электрически все три сетки.

По анодным характеристикам хорошо видно, что влияние сеточного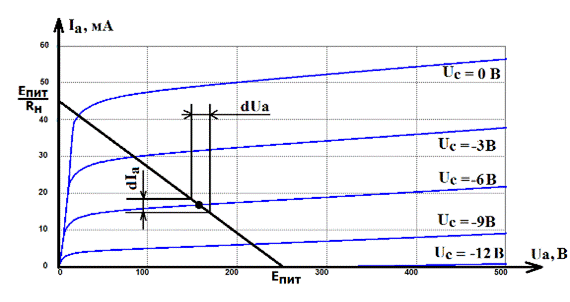

Рис. 50

напряжения на анодный ток намного сильнее, чем влияние анодного напряжения. Так, изменение напряжения на управляющей сетке с -3 В до -6 В при неизменном U_a = 100 В уменьшит I_а на 14 мА. В тоже время для изменения I_а на 4 мА потребуется приращение Δ U_a = 200 В.

Лампа с двумя сетками, т.е. с четырьмя электродами, называется тетрод, с тремя сетками – пентод. В таких лампах имеются дополнительные сетки, улучшающие электрические свойства.

Наряду со статическими характеристиками для описания свойств ламп используется следующие три дифференциальных (малосигнальных) параметра. Это крутизна анодно-сеточной характеристики S = dI_а / dU_c , внутреннее сопротивление R_i = dU_а /dI_а, коэффициент усиления по напряжению 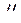= dU_а/ dU_c . Все три параметра определяются при неизменности остальных токов и напряжений [1]. Из приведённых формул следует:

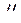= SR_i (53)

11. КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОННЫХ ЭЛЕМЕНТОВ

11.1. Компьютерная модель диода

Компьютерное моделирование электронных элементов заключается в поиске их эквивалентных схем и математических описаний, делающих возможным достаточно точный компьютерный анализ сложных схем с такими элементами.

Сегодня количество элементов в интегральных схемах может достигать 10⁹ и более. Примерно столько же уравнений в описывающей схему системе уравнений. Решение таких систем иногда невозможно даже с использованием суперкомпьютеров. Поэтому разработка компьютерных моделей элементов – это всегда компромисс между их точностью и сложностью [4].

Рассмотрим возможности моделирования полупроводникового диода на примере диода на основе p-n перехода.

Простейшей компьютерной моделью полупроводникового диода является идеальный электронный ключ, обладающий нулевым сопротивлением при прямом напряжении и бесконечным – при обратном. Такая модель отражает главное свойство диода – одностороннюю проводимость. Однако при этом не учитывается наличие прямого и обратного сопротивлений, их нелинейность, наличие ёмкости p-n перехода и другие важные его свойства.

Более совершенной является модель, основывающаяся на формуле Шокли (см. разд. 4.3):

, I = I₀(expU/j_T – 1)

Диод при этом моделируется как зависимый источник тока. Зависимость тока I от приложенного напряжения U описывается формулой Шокли (22).

Но и такая модель не отражает важнейших свойств реального диода: возникновение пробоя при обратном напряжении, наличие наклона начальной части обратной ветви ВАХ, вырождение экспоненты в линейную зависимость тока от напряжения в области больших прямых токов (рис. 51). Кроме того, эта модель не учитывает инерционные свойства диода: согласно (22), ток диода не зависит от частоты и времени, т.е. его частотные и импульсные свойства идеальны.

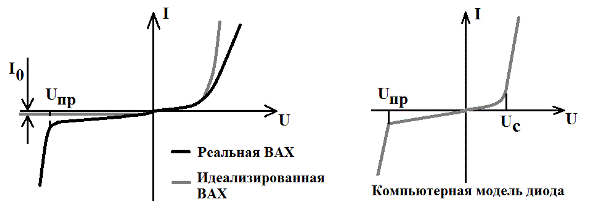
Рис. 51

Более точной, но и более сложной является модель на основе эквивалентной схемы рис. 52 и системы уравнений (54), (55), (56):

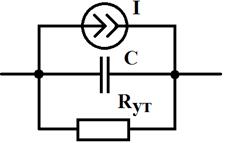
Рис. 52

(U – U_пр)/R_пр при U < U_пр (54)

I = I₀(exp(U/j_T – 1) при U_пр £ U £ U_C (55)

^I_с^{+ (U– U}_C^)/R_б^при^{U >U}_C⁽⁵⁶⁾

Здесь диод также моделируется зависимым источником тока, однако эта зависимость описывается не одним, а тремя уравнениями. Это позволяет отобразить два близких к прямой линии участка ВАХ простейшими уравнениями первой степени. Это участок пробоя, уравнение (54) и линейная часть ВАХ при прямом напряжении, уравнение (56). Уравнение (55) – уравнение Шокли, которое хорошо описывает начальную часть ВАХ диода при прямом и небольших обратных напряжениях.

Добавление в эквивалентную схему сопротивления утечки R_ут позволяет придать наклон допробойной части ВАХ при обратном напряжении и приблизить ВАХ модели к ВАХ реального диода. Так как обратный ток очень мал, добавление R_ут практически не изменяет положение остальных частей ВАХ.

Частотные и импульсные свойства диода учитываются введением в эквивалентную схему полной емкости диода С:

C = C_бар + C_дф (57)

где барьерная C_бар и диффузионная C_дф ёмкости p-n перехода описываются обычными формулами (16) и (17).

Данная модель стала основой для моделей бóльшей точности и сложности.

11.2. Компьютерная модель транзистора

В качестве примера компьютерной модели транзистора рассмотрим модель БТ с n-p-n структурой. Её прототип изображён на рис. 53:

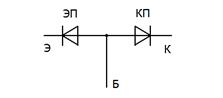
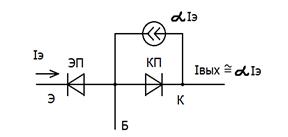
Рис. 53 Рис. 54

Здесь диоды моделируют эмиттерный (ЭП) и коллекторный (КП) переходы. При надлежащем выборе параметров этих диодов можно получить точное воспроизведение входной и выходной характеристик. Однако такая «модель» не отражает главное в процессах в БТ: взаимодействие переходов. В частности, при любом значении входного тока в ЭП выходной ток в КП не появляется.

Поэтому естественным шагом является введение в эквивалентную схему зависимого источника выходного тока αI_э, ток которого пропорционален входному току I_э,рис. 54.

Такая модель отражает важнейшее свойство БТ: в активном режиме возникает выходной ток, пропорциональный входному току. Обратные токи ЭП и КП игнорируются ввиду их малости в наиболее распространённых кремниевых транзисторах.

Дальнейшим шагом является добавление ещё одного зависимого источника тока α_iI_к, который необходим в случае инверсного режима, когда входной ток подается в открытый КП, а в закрытом ЭП появляется выходной ток, рис. 55:

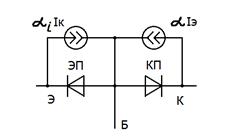
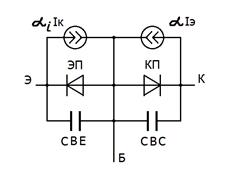
Рис. 55 Рис. 56

И хотя инверсный режим не применяется, как малоэффективный (α >> α_i) , он иногда возникает в реальных схемах и полноценная модель должна это отражать.

Следующим шагом является учёт ёмкости переходов, что обеспечивается добавлением параллельно диодам полной ёмкости КП С_КП и полной ёмкости ЭП С_ЭП, рис. 56.

Модель пополнится уравнениями, учитывающими то, что ёмкость p – n перехода при прямом напряжении диффузионная, при обратном - барьерная. Та и другая зависят не только от знака приложенного напряжения, но и от его величины.

Дальнейшее уточнение модели связано с необходимостью учёта активного сопротивления эмиттерной области R_э, базовой области R_б и коллекторной областей R_к, рис. 57. R_э - сопротивление наиболее легированной области, в связи с чем это сопротивление часто принимается равным нулю. Много большую величину имеет сопротивление базы R_б, в связи с обязательно слабым легированием этой области. Сопротивление R_к учитывают в ключевом режиме, т.к. оно влияет на сопротивление открытого состояния.

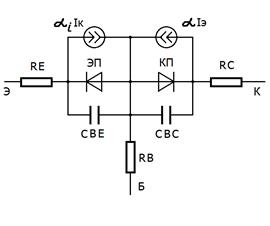
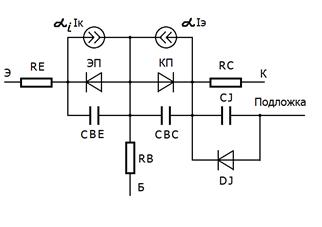
Рис. 57 Рис. 58

Поскольку БТ применяется преимущественно в интегральных схемах, между его коллекторным слоем и кристаллом ИС существует p-n переход. Поэтому модель дополняют ещё одним диодом DJ с его барьерной ёмкостью CJ, которые отражают существование этого перехода в интегральной схеме, рис. 58:

Рассмотренная модель получила название модели Эберса- Молла (по имени создателей).

Может оказаться необходимым учёт и других особенностей БТ. Это уточнённые температурные свойства, шумовые свойства, особенности конструкции и размеров. Общее число параметров модели БТ в профессиональных программах компьютерного моделирования электронных схем приближается к 100.

12. ШУМЫ ЭЛЕКТРОННЫХ ПРИБОРОВ

Напряжения и токи в электронных приборах подвержены случайным изменениям, флуктуациям. Они воспринимаются как шумовая составляющая полезных сигнальных токов и напряжений. В условиях слабых сигналов, например, в протяжённых каналах связи (спутниковая связь, оптоволоконные и кабельные линии связи) шумы часто являются главной причиной ошибок и искажений при передаче информации.

Существуют два основных вида шумов электронных приборов: тепловой шум и дробовый шум.

Тепловой шум возникает вследствие хаотического теплового движения носителей заряда. В любом сечении проводника или полупроводника, в любой отрезок времени, суммарный заряд, перенесённый слева направо отличается от заряда, перенесённого справа налево. Это неустранимое отличие ΔQ означает существование случайного по величине и направлению шумового тока i_ш.т = ΔQ/Δt. Шумовой ток существует вне зависимости от внешнего напряжения. Он создаёт шумовое напряжение u_ш.т = i_ш.тR на любом объекте c активным сопротивлением R. «Шумит» любое сопротивление - сопротивление канала МДП транзистора, сопротивление областей БТ, сопротивление обыкновенного резистора.

Типичная временная диаграмма u_ш.т изображена на рис. 59.

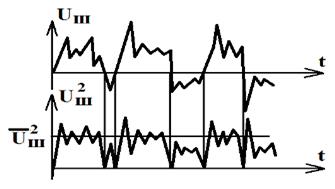
Рис. 59

Очевидно, что среднее во времени значение ūш.т = 0. Поэтому количественно тепловой шум оценивается среднеквадратичным значением напряжения шума ū_ш.т²:

ū_ш.т² = 4kTRΔf (58)

Здесь k – постоянная Больцмана, T – абсолютная температура, Δf – полоса частот, в которой шум воспринимается.

Из (57) следует, что тепловой шум можно ослабить следующими способами:

- уменьшением температуры электронных устройств или их частей (иногда применяется);

- применением в электронных устройствах элементов с минимальным сопротивлением (применяется);

- уменьшением полосы пропускания канала связи Δf.

Последнее находится в противоречии с потребностью в широкополосных каналах связи, обеспечивающих бóльшую скорость передачи информации (например, широкополосный интернет). Однако в узкополосных, «медленных» каналах достигается лучшее отношение сигнал/шум. Именно поэтому одно фото с далёкой космической станции может предаваться в течение многих часов.

Дробовый шум возникает при протекании тока в различных объектах – транзисторах, диодах, электронных лампах. Так, количество носителей в каждую единицу времени, пресекающих открытый m-n, p-n переход или пространство между анодом и катодом всегда неодинаково. Отличие может быть очень небольшим, может быть, всего на несколько электронов больше или меньше. Тем не менее, это означает, что ток в таких объектах флуктуирует, т.е. имеет дробовую шумовую составляющую i_ш.д.

Строго говоря, из-за наличия флуктуаций, постоянные токи в электронных элементах невозможны даже при постоянных напряжениях.

Временные диаграммы и подход к количественной оценке дробового шума аналогичны тем, что относятся к тепловому шуму. Среднеквадратичный дробовый шумовой ток вычисляется по формуле:

i_ш.д² = 2qIΔf (59)

Здесь q – элементарный заряд, I – ток в объекте.

Уменьшение дробового шума путем уменьшения токов транзисторов сопровождается уменьшением их усиления и возможно только в некоторых пределах. Поэтому, как и в случае теплового шума, главным способом уменьшения проявлений дробового шума является уменьшение Δf.

При компьютерном моделировании шумовых процессов в электронных схемах ко всем сопротивлениям последовательно с ними подключаются источники шумового напряжения. Ко всем контактам (переходам), в которых протекает ток, параллельно подключаются источники шумового тока [1, 5, 6].

СПИСОК ЛИТЕРАТУРЫ

1. Электронные, квантовые приборы и микроэлектроника / Под ред. Н.Д. Фёдорова. – М.,Радио и связь, 1998.

2. Степаненко И.П. Основы микроэлектроники. – М., Сов. радио,1980. – 423 с.

3. Николотов В. И. Физические основы электроники: Учебное Пособие. – М.: Инсвязьиздат, 2003. –91 с.

4. Власов В.П., Каравашкина В.Н. Практикум по курсу «Физические основы электроники» 2015г.

5. Смирнов Ю.А., Соколов С.В., Титов Е.В., Физические основы электроники: Учебное пособие для вузов. – СПб.: Лань, 2013. – 599с.

6. Шишкин Г.Г., Шишкин А. Г., Электроника. Учебник для вузов. – М.: Дрофа, 2009. – 704с.

⇐ Предыдущая 1 2 3 456 Следующая ⇒