Примеры решения задач .. Решение.. V0x=V0cosα; V0y=V0sinα.. Пусть от начала движения до момента встречи пройдет время. t=S =S* cosα.. За это время тело из точки А опуститься на величину. а тело из точки В поднимется на высоту. h=V0ytͨ

Примеры решения задач .

Снаряд вылетел из орудия под некоторым углом к горизонту и находился в воздухе 10 с. Максимальная высота подъёма снаряда?

Решение.

Максимальная высота:
H= *sin²α / (2*g)
Время полета:
t=2* 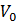*sinα /g
Отсюда:
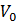*sinα=g*t/2=10*10/2=50 м/с
H=50²/(2*10)= 125 м
Ответ : 125 м

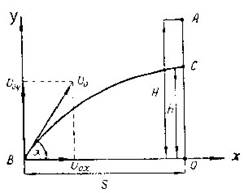2.Из точки А свободно падает тело. Одновременно из точки В под углом α к горизонту бросают другое тело так, чтобы оба тела столкнулись в воздухе. Показать, что угол α не зависит от начальной скорости 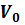тела, брошенного из точки В, и определить этот угол, если = .

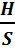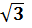Оба тела могут встретиться на линии ОА (см. рис.) в точке С. Разложим скорость V0 тела, брошенного из точки В, на горизонтальную и вертикальную составляющие:

V0x=V0*cosα; V0y=V0*sinα.

Пусть от начала движения до момента встречи пройдет время

t=S =S* cosα.

За это время тело из точки А опуститься на величину

H−h = g 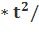2,

а тело из точки В поднимется на высоту

h=V0yt−g 2= sinα*t−g* 2.

Решая последние два уравнения совместно, находим

H=V0*sinα*t.

Подставляя сюда ранее найденное время, получим

tgα=H/S=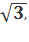

т.е. угол бросания не зависит от начальной скорости.

α=60⁰

Задача 3.

С башни брошено тело в горизонтальном направлении со скоростью 40 м/с. Какова скорость тела через 3 с после начала движения? Какой угол образует с плоскостью горизонта вектор скорости тела в этот момент?

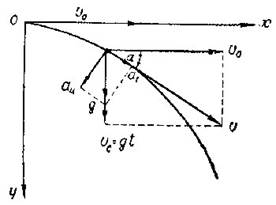Тело одновременно участвует в двух движениях: равномерно в горизонтальном направлении со скоростью V0 и в свободном падении со скоростью Vy=g*t. Тогда полная скорость тела есть

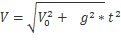
Направление вектора скорости определяется углом α.

Из рисунка видим, что

Cos α = 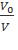= = 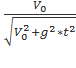0.8 . Отсюда α=37⁰

12 3 Следующая ⇒