Двудольный граф. Эйлеров граф

Двудольный граф

Граф называется двудольным, если множество его вершин можно разбить на два подмножества так, чтобы никакое ребро не соединяло вершины одного и того же подмножества.

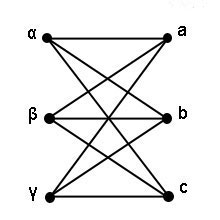
Пример 1.Построить полный двудольный граф.

Полный двудольный граф состоит из двух множеств вершин и из всевозможных звеньев, соединяющих вершины одного множества с вершинами другого множества (рисунок ниже).

Эйлеров граф

Мы уже касались задачи о кёнигсбергских мостах. Отрицательное решение Эйлером этой задачи привело к первой опубликованной работе по теории графов. Задачу об обходе мостов можно обобщить и получить следующую задачу теории графов: можно ли найти в данной графе цикл, содержащий все вершины и все рёбра? Граф, в котором это возможно, называется эйлеровым графом.

Итак, эйлеровым графом называется граф, в котором можно обойти все вершины и при этом пройти одно ребро только один раз. В нём каждая вершина должна иметь только чётное число рёбер.

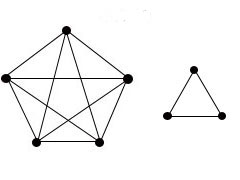
Пример 2.Является ли полный граф с одинаковым числом n рёбер, которым инцидентна каждая вершина, эйлеровым графом? Объяснить ответ. Привести примеры.

Ответ. Если n - нечётное число, то каждая вершина инцидентна n-1 рёбрам. В таком случае данный граф является эйлеровым графом. Примеры таких графов на рисунке ниже.

⇐ Предыдущая 123 4 Следующая ⇒