
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные виды графов. Ориентированные и неориентированные графы. Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Основные виды графов
- Ориентированные и неориентированные графы
- Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
- Двудольный граф
- Эйлеров граф
- Регулярный граф
- Гамильтонов граф
- Взвешеный граф
- Графы-деревья
Виды графов могут определяться общими принципами их построения (таковы, например, двудольный граф и эйлеров граф), а могут зависеть от тех или иных свойств вершин или рёбер (например, ориентированный и неориентированный граф, обыкновенный граф).
Ориентированные и неориентированные графы
Графы, в которых все рёбра являются звеньями (порядок двух концов ребра графа не существенен), называются неориентированными.
Графы, в которых все рёбра являются дугами (порядок двух концов ребра графа существенен), называются ориентированными графами или орграфами.
Неориентированный граф может быть представлен в виде ориентированного графа, если каждое его звено заменить на две дуги, имеющие противоположные направления.
Графы с петлями, смешанные графы, пустые графы, мультиграфы, обыкновенные графы, полные графы
Если граф содержит петли, то это обстоятельство специально оговаривают, добавляя к основной харатеристике графа слова "с петлями", например, "орграф с петлями". Если граф не содержит петель, то добавляют слова "без петель".
Смешанным называют граф, в котором имеются рёбра хотя бы двух из упомянутых трёх разновидностей (звенья, дуги, петли).
Граф, состоящий только из голых вершин, называется пустым.
Мультиграфом называется граф, в котором пары вершин могут быть соединены более чем одним ребром, то есть содершащий кратные рёбра, но не содержащий петель.
Граф без дуг (то есть неориентированный), без петель и кратных рёбер называется обыкновенным. Обыкновенный граф изображён на рисунке ниже.
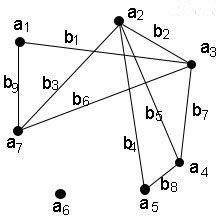
Граф заданного типа называют полным, если он содержит все возможные для этого типа рёбра (при неизменном множестве вершин). Так, в полном обыкновенном графе каждая пара различных вершин соединена ровно одним звеном (рисунок ниже).
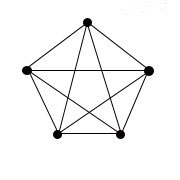
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|