Хелпикс

Главная

Контакты

Случайная статья



Три «особых» случая при решении систем линейных уравнений

⇐ ПредыдущаяСтр 2 из 2


Три «особых» случая при решении систем линейных уравнений

1) система линейных уравнений имеет единственное решение(система совместна и определена).Условия: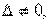  

2) система линейных уравнений имеет бесчисленное множество решений

(система совместна и не определена)

Условия:

* ,

** ,

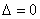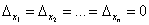3) система линейных уравнений решений не имеет(система несовместна)

Условия:

*

** .

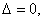
Итак, система m линейных уравнений с n переменными называется несовместной, если у неё нет ни одного решения, и совместной, если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой, а более одного – неопределённой.

Решите системы методом Крамера системы линейных уравнений:


1)

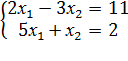
2)

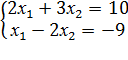
3)

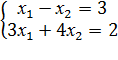
4)

5)

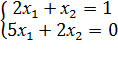
6)

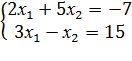
7)

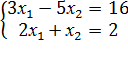
8)

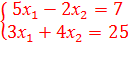
9)

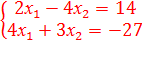
10)

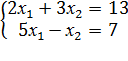
11)

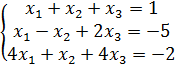
12)

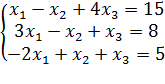
13)

 

14)

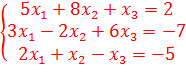
15)

16)

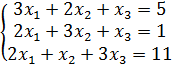
17)

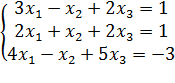
18)

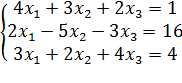
19)

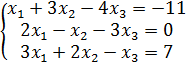
20)

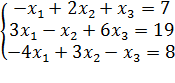
21)

22)

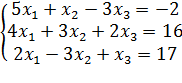
23)

 


⇐ Предыдущая12
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.