
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрические функции числового аргумента. Вычисление значений тригонометрических выражений.
Тригонометрические функции числового аргумента. Вычисление значений тригонометрических выражений.
План
1. Определение тригонометрических функций острого угла.
2. Определение тригонометрических функций любого аргумента.
3. Знаки тригонометрических функций.
4. Периодичность тригонометрических функций.
5. Четность, нечетность тригонометрических функций.
6. Формулы приведения 6(а) таблица значений.
7. Тригонометрические тождества.
Любой угол измеряется либо в градусной мере измерения (единица измерения – градус), либо в радианной (единица измерения – радиан). Один дуговой градус – это 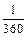 часть окружности. Один угловой градус – это центральный угол, опирающийся на дуговой градус. Радианная мера угла – это отношение длины дуги к радиусу этой дуги. Радиан – это центральный угол, опирающийся на дугу, равную длине радиуса этой дуги. Окружность содержит
часть окружности. Один угловой градус – это центральный угол, опирающийся на дуговой градус. Радианная мера угла – это отношение длины дуги к радиусу этой дуги. Радиан – это центральный угол, опирающийся на дугу, равную длине радиуса этой дуги. Окружность содержит 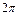 радиан.
радиан.
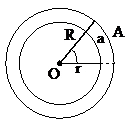
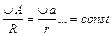 – радианная мера угла
– радианная мера угла
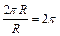 радиан
радиан
1 рад 
Для перехода от градусной меры измерения угла к радианной и наоборот можно пользоваться формулами: 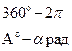
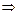
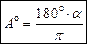 ;
; 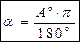
Например:
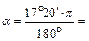
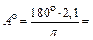 1) Дано:
1) Дано: 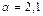 2) Дано:
2) Дано: 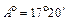
Найти: 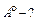 Найти:
Найти: 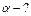
В прямоугольном треугольнике. Для произвольного угла

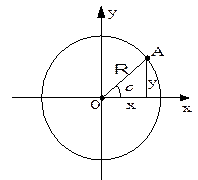
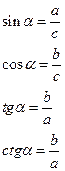

Основные тригонометрические тождества
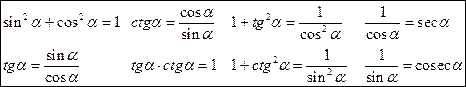
Из определения:
|

функции ограниченные
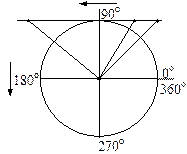 | |||||||
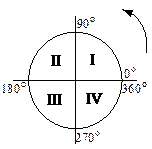 | |||||||
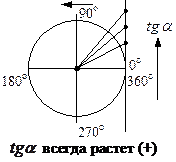 | |||||||
| |||||||
|
| Знаки функций по четвертям | ||||
| I | II | III | IV | |
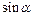
| + | + | – | – |
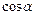
| + | – | – | + |
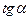
| + | – | + | – |
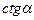
| + | – | + | – |
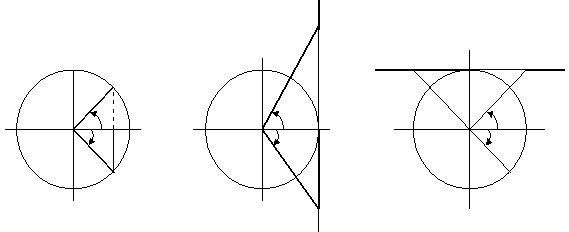
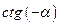 | |||||||||||||||||||||||
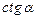 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
 | |||||||||||||||||||||||
 | 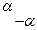 | ||||||||||||||||||||||
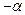 | |||||||||||||||||||||||
| |||||||||||||||||||||||
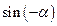 | 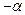 | ||||||||||||||||||||||
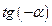 | |||||||||||||||||||||||
| |||||||||||||||||||||||

|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
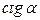 всегда убывает (+)
всегда убывает (+)
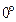
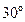
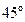
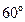
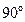
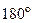
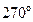
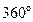
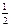
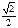

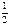
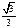
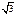
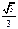
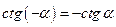 (нечётная)
(нечётная)
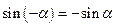 (нечётная)
(нечётная)
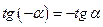 (нечётная)
(нечётная)