Теріс емес бүтін сандарға қолданылатын амалдарды талдау

Математиканың жалпы ұғымдарын талдау. Логикалық схема 2. Теріс емес бүтін сандарға қолданылатын амалдарды талдау. Концептуалды карта 3. Теңдеулер. Теңсіздіктер. Функицялар. Концептуалды карта

Математиканың жалпы ұғымдарын талдау. Логикалық схема Математика ғылымы,басқа ғылымдар сияқты бізді қоршаған дүниені,табиғи және қоғамдық құбылыстарды,олардың ерекше қасиеттерін зерттейді.Мысалы,геометрия курсында заттардың басқа қасиеттеріне көңіл аудармай (түсі,массасы,қаттылығы,т.б.) олардың формалары мен өлшемдерін қарастырамыз.Сондықтан геометрияда «зат» деген сөздің орнына «геометриялық фигура» деген сөз қолданылады.,бұрыш,дөңгелек,шаршы – бұлардың барлығы геометриялық фигуралар.Олар жалпылама ұғымдар да абстракциялау ( жалпылау) нәтижесі болып табылады.Жалпы, кез келген математикалық обьектілер – бізді қоршаған дүниедегі заттар мен құбылыстардың басқа қасиеттерінің ішінен сандық және кеңістік қасиеттерін бөліп алу нәтижесі.Ендеше, математикалық оьектілер геометриялық фигуралар,сандар, т.б. шындық дүниеде жоқ.Олардың барлығы қоғамның даму тарихы барысында пайда болып, адамның тек қиялында өмір сүреді. Бұған қоса математикалық ұғымдардың жасалуында сәйкес заттардың көптеген қасиеттерін жалпылаумен қатар, іс жүзінде ешбір затта жоқ қасиеттерді де меншіктеу болады.Мысалы,түзу деп аталатын математикалық обьектіде нақты заттардың ұзыннан – ұзақ созылу қасиетімен бірге оның өмірде кездесетін заттардың арасында бірде – біреуі ие болмайтын екі жаққа да шексіз созылу қасиеті бар

Теріс емес бүтін сандарға қолданылатын амалдарды талдау

Өрнектерде теріс санның тікелей алдында қосу,көбейту,бөлу, азайту таңбалары тұрса, онда теріс сан жақшаға алынып жазыладын.

Мысалы: 9+(-7); 8:(-2); 6*(-3); 7-(-6)

Көп жағдайда теріс сан өрнектің бірінші мүшесі болса, ол жақшасыз жазылады.

Оң сандарға: 0,75; 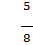; 9; 6.

Теріс сандарға: -1; - ; -4,3; -7.

Оң санғада және теріс санғада жатпайтын тек 0 саны ғана.

Екі теріс санның көбейтіндісі –оң сан.

Мысалы: (-0,2) * (-1,5)=|-0,2 | *|-1,5|=0,3

Теріс нақты сандар жиыны мен оң нақты сандар жиынының және санының бірігуін нақты сандар жиыны деп атап, R әрпімен белгілейді.нақты сандар мен координаттық түзудің нүктелер жиыны өзара бірмәнді сәйкестікте болады: Әрбір нақты санға координаттықтүзудің біp ғана нүктесі жене координаттық түзудің әрбір нүктесi бір ғана нақты санара сәйкес келеді. Координатасы саны болып табылатын санақ басынан нүктеге дейінгі кашықтық санның модулі деп аталады жәнеIXI түрінде белгіленеді. Сонымен,IXI={ егер 𝑥 ≥ 0, онда𝑥 егер 𝑥 < 0 онда − 𝑥 Мысалы/-7/=7, /5,5 ;/0/=0 "Кем" жене "артық" катынастарын анықтай отырып, нақты сандарды былайша салыстырады: Егер координаттық түзудің бойында a нүктесі в нүктесіне қарағанда солға қарай орналасса, онда аb болады. Бұл анықтамадан кез келген оң сан 0-ден артық, ал кез келген сан 0-ден кем болатыны шығады. "Кем" және "артық" қатынастарының анықтамасынан тағы да мынадай тұжырым жасауға болады: 1) a b сонда және тек қана сонда, егер а-b айырымы оң сан болса. Кезкелген𝑎және𝑏нақтысандарыүшін, мынакатыстардыңбіреуіжәнетекбіреyiopындалады:а < 𝑏, а > 𝑏, а − b.Нақтысандарүшінамалдаркелесіережелербойыншаорындалады. Екінактысанныңқосындысыдепкелесішарттардықанағаттандыратынсандыайтамыз: 1) Екі оң санның қосындысы қашан да оң сан болады және оң накты сандар жиынында анықталған ереже- лербойынша табылады. 2) Екі теріc санның қосындысы теріс сан; қосындның модулін табу үшін, косылғыштардың модульдерін қосу керек. Таңбалары әр түрлі екі санның косындысы модулі үлкен қосылғыштың таңбасы болады; қосындының модулін табу үшін үлкен модульден кіші модульді азайтып, үлкен модульдің таңбасын қояды. 4) Модульдері тең карама-карсы таңбалы сандардың косындысы нелге тең. ЕKI нақты санның көбейтіндісі деп келесі шарттарды қанағаттандыратын санды айтады: санның көбейтіндісі қашан да оң сан болады және ол оң нақты сандар жиынында анықталған ережелер бойынша табылады. 2) Екі теріс санның көбейтіндісi оң сан болады; сондықтан балар әр түрлі екі санның кебейтіндісі қашан да теpic сан болады; көбейтіндінің модулін табу үшін, осы сандардың модульдерін көбейту керек. Нақты сандарды азайту жене бөлу сәйкесінше қосу жане көбейтуге кері амалдар түрінде анықталады.

. Теңдеулер. Теңсіздіктер.

4х және 5х+2 түріндегі айнымалылары бар екі өрнекалайық. Оларды теңдік (=) белгісімен жалғастырыпжазсақ, онда 4x=5x+2 түріндегі сөйлем аламыз. Бұл сөйлемнің айнымалысы бар және айнымалының орны нақты мәндерді қойсақ, сөйлем пікірге айналады. Мысалы, х=1 мәнін қойғанда 4x=5х+2 сөйлемі жалған пікірге,алх=-2 мәнін қойғанда ақиқат пікірге айналады. X=1, 4•1=5•1+2 - жалған пікір X=-2, 4•(-2)=5•(-2)+2 - ақиқат пікір. Сондықтан, 4х=5х+2 сөйлемі предикат болып табылды. Мұндай түрдегі сөйлемдерді айнымалысы бар теңдік немесе бір айнымалысы бар теңдеу деп атайды.Жалпы түрде бір айнымалысы бар теңдеу ұғымын былайша анықтауға болады: Анықтама: f(x) және g(x) х айнымалысы бар және анықталу облысы х болатын екі өрнек болсын. Сонда f(x) =g(x)түріндегі пердикат бір айнымалысы бар теңдеу деп аталады. Теңдеуді ақиқат санды теңдікке айналдыратын Х, х-тің мәндері теңдеудің шешімі немесе оның түбірідеп аталады. Теңдеудің шешімдерінің жиынын табу дегеніміз - берілген теңдеуді шешу.Бір айнымалысы бар теңдеулердің бірнеше мысалынкелтірейік: l-мысал: 4x=5x+2, x𝜖R. Бұл теңдеу тек х=-2 болғанда ғана ақиқат санды теңдікке айналады. Ендеше, оның шешімдерінің жиыны {-2} 2-мысал: (x-1) (x+2)=0, бір айналысы бар бұл теңдеу х=1 және х=-2 болғанда ақиқат санды теңдікке айналады. Сонымен, бұл теңдеудің шешімдерінің жиыны: (1;-2) 3-мысал: (3х+1) 2=6х+2, х𝜖R. Егер теңдіктің бөлігіндегі жақшаны ашсақ, онда берілген теңдеу кесте 6x+2=6x+2 түрінде келеді. Алынған жазух-тің кез кел-келген мәнінде ақиқат санды теңдікке айналатынынбілдіреді. Бұл жағдайда берілген теңдеу шешімдерінің жиыны барлық нақты сандар жиыны R деп атайды. 4-мысал: (8x+1)- 2-6x+1, x𝜖R. Берілген теңдеу х-тің бірде-бір нақты мәнінде ақиқат санды теңдікке айналмайтынына Оңай көз жеткізуге болады. Сол жақтүрлендіру жасағаннан кейін 6x+2=x+1 түріндегі жазуын аламыз. Бірақ 1≠2. Бұл жағдайда берілген теңдеулердің шешімі жоқ деп айтады немесе берілген теңдеу шешімдерінің жиыны бос жиын болады. Бастауыш куре математикасындах х+а=b, a-x=b, x-a=b, х-а=b, х=b түріндегі қарапайым теңдеулер қарасты-рылады, мұндағы а, - теріс емес бүтін сандар, ал х - айнымалы. Бастауыш сыныпта теңдеу ұғымы айқын түрде берілмейді. Ол құрамында әріпті өрнек болатын теңдік түрінде де енгізіледі және сол тендікті тура санды теңдікке айналдыратын әріптің мәнін табу міндетті болып есептеледі. Тең мәндес теңдеулер Берілген теңдеуді шешу үшін оны әдетте түрлендіңіп,берілген теңдеуге қарағанда қарапайымдылау теңдеу- мен ауыстырады. Бұл процесті теңдеуді шешу тәсілі сөзімізге белгілі тәсілге келтірілгенге дейін жалғастыруға болады. Бұл табылған шешімдер берілген теңдеудің шешімі болу үшін, түрлендіру процесінде шешімдерінің жиыны бір-біріне сәйкес келетін теңдеулер алынуы керек. Мұндай теңдеулерді мәндес теңдеулер деп атайды. Анықтама: Егерекі теңдеудің шешімдерінің жиыны бір-біріне тең болса, онда мұндай теңдеулерді мәндес теңдеулер деп атайды. Мысалы, (х+1) 2=9 және(х-2) (х+4) =0 теңдеулері нақтысандар жиынында өзара мәндес. Өйткені, бұл теңдеулер{-4;2} Енді қандай түрлендірулердің берілген теңдеумен мәндес теңдеулер алуға мүмкіндік берілетіндігін анықтайық. Бұл түрлендірулер келесі теоремаларда көрініс табады. Теорема: f(x)=g(x) теңдеуі және һ(х) өрнегі Х жиынында берілген болсын. Сонда, f(x)-g(x)және f(x)-h(x) =d(x)+h(x)(2) теңдеулері Х жиынында мәндес болады. Бұл теореманы басқаша да тұжырымдауға болады: егер анықталу облысы Х болатын теңдеудің екі бөлігіне де осы Х жиынында анықталған, айнамалысы бар өрнекті қосқанда, берілген теңдеумен мәндес жаңа теңдеу аламыз. Дәлелдеуі: Т1арқылы (1) теңдеудің шешімдерінің жиынын, ал Т2 арқылы (2) теңдеудің шешімдерінің жиынын белгілейік.Егер Т1= Т2, болса, онда (1) және (2) теңдеулер мәнеес болады. Бірақ бұған көз жеткізу үшін Т1, жиынынан алынған кез келген түбір (2) теңдеудің және керісінше Т2 жиынынан алынған кез келген түбір (1) теңдеудің шешімі болатынын көрсету қажет.a - саны (1) теңдеудің шешімі болсын. Сонда а𝜖Т1, және (1) тендеуге а-ны қойғанда бұл теңдеу теңдікке айналдырады: f(a)=g(a), алһ(х) өрнегін һ(а) санды өрнегіне айналдырадыf(a) -d(а) ақиқат теңдігінің екі бөлігіне де һ(а) сандыөрнегін қосамыз. Ақиқат санды теңдіктердің қасиетіне сәйкес ақиқат санды теңдік аламыз: f(2)=h(a)=g(a)+h(a) Бұл теңдік a саны сондай-ақ (2) теңдеудің де шешімі болатындығын білдіреді. Сонымен, (1) тендеудің шешімі (2) теңдеудің де шешімі болатындығы дәлелденді, яғни 𝑇1 ∈ 𝑇2 Енді b саны (2) теңдеудің шешімі болсын. Сонда b=𝑇2және оны теңдеуге қойғанда, теңдеуді ақиқат сандытеңдікке айналдырады. f(b) -h(b) = g(b)+h(b) Осы санды теңдіктің екі бөлігіне де - h(b) санды өрнегін қоссақ, онда f(b) =h(b) ақиқат санды теңдігін аламыз. Бұл саны (1) теңдеудің шешімі болатындығын білдіреді. Сонымен, (2) теңдеудің шешімі (1) теңдеудің де шешімі болатындығы дәлелденді, яғни 𝑇!=𝑇2, 𝑇2 ∈ 𝑇1 ,𝑇1 ∈ 𝑇2олғандықтан, тең жиындардың анықтамасы бойынша 𝑇1 = 𝑇2 , ал (1) және (2)Х жиында өзара мәндес теңдеулер. Теңдеулерді шешуде көпшілік жағдайда теореманың өзі емес одан шығатын сандар қолданылады: 1. Егер теңдеудің екі бөлігіне де бірдей санды қосса,берілген теңдеуге мәндес теңдеу шығады. 2. Егер қайсыбір қосылғышты (санды өрнек немесе айнымалысы бар өрнек) теңдеудің бір бөлігінен екінші бөлігіне қарама-қарсы таңбамен ауыстырғанда берілген теңдеулермен мәндес теңдеу шығады. Теорема 2: f(x) =g(x) теңдеуді Х жиынында берілгенжәне һ(х) осы жиында анықталған және хеХ кез келгенмәнінде нөлге мәні нөлге айналмайтын өрнек болсын.Сонда f(x) = g(x) және f(x) =h(x) = g(x)+h(x) теңдеулері Xжиынында мәнде болады. Бұл теореманың дәлелдеуіне ұқсас.(Дәлелдеуін студенттерге өздік жұмыс ретінде ұсынамыз). Теоремадан теңдеулердің шешуде қолданылаты мынадай салдар шығады: Егер теңдеудің екі бөлігін де нөлден өзгеше болатын бірдей санға көбейтсе(немесе болса), онда берілген теңдеумен мәндес теңдеу аламыз. 1 𝑥 3 = 𝑥 3 теңдеуін шешіп, оны шешуде қандай теориялық заңдылықтар қолданылатындығын анықтайық. Теңдеудің шешужолы Қолданылған теориялық Заңдылықтар 1. Теңдеудің сол және оң жақ бөліктеріндегі өрнектерді ортақ бөлімге келтірейік: Теңдеудің сол жақ бөлігіндегі өрнекті теңбе-тең түрлендіруді орындап, берілген теңдеуге мәндес теңдеуалдық 2. Ортақ бөлімді тастап Теңдеудің екі жақ бөлігін де жазамыз: 6-2x=x Теңдеудің екі жақ бөлігін де 6-ға көбейттік (12 теорема бойынша). Сонда берілген теңдеумен мәндес теңдеу шықты, 3.-2х өрнегін теңдеудің оң жақ бөлігіне шығарамыз:6=x+2x 1 теоремадан шығатын салдарды қолданып, теңдеудің екі бөлігіне де 2х өрнегін (барлық нақты сандар жиынында анықталған) қосып берілген теңдеумен мәндес теңдеу аламыз. 4. Теңдеудің оң бөлігіндегі ұқсас мүшелерді біріктіреміз: 6-3х Теңбе-тетүрлендіруді орындап алдыңғы теңдеумен,яғни берілген теңдеумен мәндес теңдеу аламыз. 5. Теңдеудің екі бөлігін де салдарды 3-ке бөлеміз: х= 2 2 теоремадан шығатын пайдаланып теңдеудің екі бөлігін де 6санына көбейтіп, берілген теңдеумен мәндес теңдеу аламыз Сонымен, берілген теңдеудің шешімдерінің бір ғана сан. Ол 2 саны, яғни . Енді х(х1)=2x, теңдеуін алайық. Кейбір жағдайда оны оқушылар былай шешеді: теңдеудің екі бөлігін де х-ке бөліп, х-1-2 теңдеуін алады. Бұдан х= 3 екенін табады және теңдеудің шешімдерінің жиыны (3)деп қорытынды жасайды. Бірақ берілген теңдеу дұрыс шешілген бе? x(x-1)=2x теңдеуінақиқат пікірге айналдыратын х-тің барлық мәндері та-былады ма? X=0 болғанда берілген теңдеу 0 (0-1)=2 • 0 түріндегі ақиқат санды теңдікке айналатынын көру қиын емес.Ендеше, 0 саны берілген теңдеудің тағы бір түбірі болады. Бұл түбір неліктен табылмай қалуы? Бар мәселе,x-1=2 теңдеуінің 2(x-1)=2 х теңдеуімен мәндес болмайтындығында, яғни 2 теореманың шарты орындалмайды,өйткені біз берілген теңдеудің екі бөлігін де нақты сандар жиынында толық анықталмайтын, дәлірек айтқанда,x=0 болғанда мағынасы болмайтын - өрнегіне көбейту арқылы соңғы теңдеуді алдық. X(x-1)=2x теңдеуін қалайша дұрыс шешуге болатындығының бір ғана жолын көрсетейік. Теңдеуді шешу жолы Қолданылған теориялық заңдылықтар 2x өрнегін теңдеудің оң жақ 1 теоремадан шығатын сандарды бөлігінен сол жақ ауыстырамыз: x(x-1)-2x=0 1 теоремадан шығатын сандарды Бөлігінен сол жақ бөлігіне пайдаланып, берілген теңдеумен мәндес теңдеу аламыз 2. Теңдеудің сол жақ бөлігінде х-ті жақшаның сыртында ұқсас мүшелерін біріктіреміз: x(x-3)-0 Теңбе-тең түрлендірулерді орындайық. Олар теңдеулердің мәндесұқсас мүшелерін біріктіреміз: тігін бұза алмайды. 3. Екі көбейткіштің көбейтіндісі Бірнеше көбейткіштердің ең болмағанда біреуі нөлге тең болғанда ғана тең болады. Сондықтан х= 0 немесе x-3=0 Бірнеше көбейткіштердің нөлге Шартын қолданып, берілген теңдеумен мәндес теңдеу аламыз. 4. 3 санын теңдеудің оң жақ бөлігіне шығарып, алатынымыз: х= 0 немесе пайдаланып, x=3 | 1 теоремадан шығатын салдарды пайдаланып x-3=0 мәндес теңдеу аламыз. Сонымен, берілген теңдеудің шешімдерінің жиыныекі саннан 0 және 3-тен тұрады, яғни (0,3). 1 және 2 теоремалардың шарттарын орындалмау теңдеу түбірлерінің жоғалуына ғана емес, сондай-ақ бөгде түбірлердің де пайда болуына әкелетіндігін ескертеміз. Қандай түбірлердің бөгде түбірлер деп атайды? f. (x) =d (x) (1) және f, (x) = d, (x) екі теңдеу берілген болсын. Егер (1) теңдеудің барлық түбірлері (2) теңдеудің түбірлері болса, онда (2) теңдеу (1) теңдеуден шынады деп немесе (2) теңдеу (1) теңдеудің салдары деп айтуғатубірлері (1)болады. Егер (2) теңдеудің түбірлері (1) теңдеуді қанағаттандырмайтын болса, онда бүл түбірлер (1) теңдеу үшін бөгде түбірлер болады. Мысалы, 5𝑥−15 (х+2)(𝑥−3) == 0 теңдеуін шешкенде теңдеудің екі бөлігін де (x+2) (x-3)-ке көбейтіп, теңдеудің бөлімінен құтыламыз да, 5х-15=0 екенін аламыз. Бұдан x=3 бірақ х==3 болғанда бөлшегінің бөлімі нөлге айналып кетеді. Сондықтан х=3 саны берілген теңдеу үшін бөгде түбір болып есептеледі. Жалпы, егер теңдеуді шешу кезінде оны оның салдарымен ауыстырса (мәндес теңдеумен емес), онда салдар-теңдеудің барлық түбірлерін табу керек, ал содан кейіноларды берiлген тендеуге койып, тексеру керек. Бөгде түбiрлердi алып тастайды. Тендеулердi шешкенде, бегде тубiрлердiн пайда болу кұбылысы, түбiрлердi жогалтпауға қарағанда «Қауіпті»емес.Сондыктан тендеулердi шешу кезiнде алдымен мендестiк туралы теоремалардын дурыс колданылуына назар аудару керек. Бастауыш курс математикасында тендетлердi шешудан теориялык негiзi анал компоненттерi мен нәтижесi арасындагы байланыс болып табылады. Мысалы,(x 9):24=3 тендеуiн шешу мынадай турде негiзделедi: Бөлінгіш белгісіз болғандыктан, табу үшiн бөлгiштi белiндiнiңмәніне кебейту керек: x * 9=24 3немесе х 9=72. Белгiciз кебейткiштi табу ушiнкебейтiндiнiн менiн белгiлi кебейткiшке белу керек 72:9 немесе х=8. Ендеше, берiлген тендеудiн шешiмi 8саны болып табылады Бір айнымалысы бар теңсіздіктер. Тең мәндес теңсіздіктер 2х+7>10-х, х2+7хd(x) немесе f(x)10 және 2x>3 теңсіздіктерді тең мәндес, өйткені, олардың шешімдерінің жиыны (1,5;+). Теңсіздіктердің мәндестігі туралы теоремалар және олардың шығатын салдарлар іс жүзінде теңдеулердің мәндестігі туралы теоремаларға ұқсас және де олардың дәлелдеулері 1 теореманың дәлелдеуіне ұқсас жүргізіледі. Теорема 3 : f(x)>d(x) теңсіздігі Хжиынында берілген және h(x) осы жиында анықталған өрнек болсын. Сонда f(x)>g(x) және f(x)+h(x)>g(x)+h(x) теңсіздіктері Х жиынында мәндеа болады. Бұл теоремадан теңсіздіктерді шешде жиі қолданылатын мынадай салдар шығады. 1) Егер f(x)>g(x) теңсіздігінің екі бөлігінде де бірдей d санын қоса,онда берілген теңсіздікке тең мәндес f(x0+d>g(x)+d теңсіздігін аламыз 2) Егер қандайда бір қосылғышты (санды өрнекті немесе айнымалысыбар өрнекті ) оның таңбасын қарама-қарсы өзгертіп ,теңсіздіктің бір бөлігінен екінші бөлігіне көшірсе ,онда берілген теңсіздікке мәндес теңсіздік шығады. Теорема 4:f(x)>g(x) X жиынында берілген теңсіздік және h(x) осы жиында анықталған және де х? Х барлық х үшін h(x) >0 болсын.Сонда f(x)>g(x) және f(x) h (x)>g(x) теңсіздіктері тең мәндес болады. Бұл теоремада мынадай салдар шығады: Егер f(x)>g(x) теңсіздігінің екі бөлігін де теріс таңбалы d нақты санына көбейту және теңсіздік таңбасын қарама-қарсыға өзгертсе,онда f(x)•dg(x) X жиында берілген теңсіздік және f(x) осы жиында анықталған және де xϵX барлық х үшін f(x)g(x) және f(x) h(x)g(x) теңсіздігінің екі бөлігіндеде теріс таңбалы d нақты көбейтса және теңсіздік таңбасын қарама-қарсыға өзгерсе ,онда 𝑓(𝑥) • 𝑑-2 . 5- теоремадан шығатын салдарды қолданып,берілген теңсіздікпен мәндес теңсіздік аламыз Х>-2 теңсіздігінің шешімі (-2;+∞)аралық болып табылады.Сонымен,-12-7х

12 3 Следующая ⇒