Рис. 1.2. Кубический объем из N ячеек, каждая из которых может содержать только один (красный или синий) шарик

Рис. 1.2. Кубический объем из N ячеек, каждая из которых может содержать только один (красный или синий) шарик

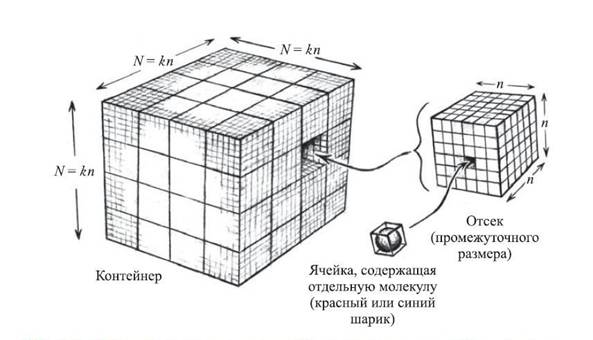
Рис. 1.3. Кубический объем в виде решетчатого контейнера, составленного из k3 кубических ячеек, или отсеков, каждый из которых имеет объем n × n × n ячеек

Предположим, что число молекул в системе очень велико (но не бесконечно!), а сами молекулы моделируются микроскопическими шариками (красного и синего цвета). Каждый шарик может занимать лишь дискретное положение в центре крошечного кубика (назовем его клеткой, или ячейкой, или отсеком). На такие кубики разделен объем системы, как показано на рис. 1.2. Для упрощения расчетов также положим (хотя это и не играет принципиального значения), что в соответствии с рисунком система имеет форму огромного куба, состоящего из N³ = N × N × Nтаких отсеков, каждый из которых, повторю, вмещает только одну молекулу красителя.

Предложенная простая модель позволяет количественно оценить «цвет» какого-либо участка объема рассматриваемой системы, исходя из заполнения отдельных ячеек. Для этого усредним «окраску» участков куба по следующей схеме. Введем в рассмотрение объем некоторого куба, который, с одной стороны, намного меньше, чем весь объем системы, а с другой — значительно превышает по размерам объем отдельной ячейки. Иными словами, как показано на рис. 1.3, в этом промежуточном объеме содержится очень большое количество индивидуальных ячеек для молекул или атомов, но одновременно он намного меньше объема всей системы в целом. Длина ребра такого куба в n раз превышает длину ребра элементарной ячейки (так что он содержит n³= n × n × n ячеек), но при этом число n(остающееся очень большим) существенно меньше общего числа N молекул в системе. Таким образом, справедливо неравенство

N >> n >> 1.

Для удобства я буду полагать (хотя это условие не играет никакой роли в расчетах), что имеется число целое k, с помощью которого можно записать простое соотношение:

N = kn,

где k³= k × k × k соответствует полному числу микрообъемов (назовем их зернами) промежуточного размера для рассматриваемой системы.

Читатель легко поймет идею метода, который связан с подразделением системы на «отсеки» промежуточного размера, состоящие из микроскопических, атомарных ячеек. Каждая ячейка слишком мала для определения индивидуальной «окраски», но для отдельных отсеков промежуточного размера мы уже можем определить усредненный цвет исходя из соотношения красных и синих шариков внутри этого отсека или зерна. Обозначив число красных и синих шариков буквами r и b (по первым буквам английских прилагательных red и blue; а сумма r + b равняется, естественно, величинеn³), мы сможем количественно оценить оттенок каждого отсека по отношению параметров r и b. Соответственно, при таком подходе можно говорить, что какой-то конкретный отсек имеет красный или синий цвет — в зависимости от того, насколько отношение параметров r/bв данном отсеке выше или ниже единицы (понятно, что при отношении r/b = 1 отсек имеет именно «равновесный», пурпурный цвет).

Будем считать, что окраска какого-то отсека (зерна) кажется нам однородно пурпурной лишь в тех редких случаях, когда соотношение r/b лежит в узких пределах от 0,999 до 1,001, т. е. соответствует точности измерений около одной десятой процента. На первый взгляд это условие представляется очень жестким и сложным (исходя из того, что оно должно выполняться для каждого из огромного числа n³ = n × n × n таких отсеков, или зерен), однако это условие иногда (при очень большом количестве шариков, в нашем случае молекул) неожиданно выполняется с удивительной легкостью! Дело в том, что в рассматриваемых системах мы сталкиваемся с проблемами распределения чрезвычайно большого, практически совершенно немыслимого числа частиц, для которых характерны необычные с практической точки зрения закономерности, и это требует правильного подбора масштабов используемых характерных параметров. Так, обычная банка краски (пример большой системы) содержит в среднем 10²⁴ молекул, вследствие чего число N вполне может равняться 10⁸. Если в качестве образца ячейки (отсека, или зерна, промежуточного размера) взять, например, отдельный пиксель изображения на высококачественной цветной фотографии, имеющий размеры всего 10^–2 см, то в этом случае вполне разумно приписать числу k значение 10³. Для приведенных величин легко рассчитать вероятности различных сочетаний в рассматриваемой нами задаче, когда требуется получить однородную пурпурную окраску из синих и красных шариков в отдельных ячейках на рис. 1.1 из смеси их равных количеств N³/2. Например, можно легко показать, что для указанных чисел N = 10⁸ и k = 10³ (для этих чисел n = 10⁵) восприятие однородного пурпурного цвета обеспечивается примерно 10^{23 570000 000000 000000 000000}сочетаниями положений молекул. При этом существует всего около 10^{46 500000 000000}таких особых расположений молекул, при которых все синие шарики оказываются в верхней части объема, а все красные — в нижней. Таким образом, при совершенно случайном разбросе положений молекул вероятность возникновения однородной пурпурной окраски оказывается очень высокой, а вероятность обнаружения всех синих шариков вверху — ничтожно малой (всего около 10^{–23 570000 000000}), причем эта величина почти не изменится, если мы потребуем, чтобы вверху располагались не все синие шарики, а лишь 99,9 % от их количества.

Указанная теоретическая схема позволяет нам рассматривать энтропию в качестве характеристики или меры описываемых вероятностей, иными словами, как меру вероятности расположения шариков, соответствующего одинаковой «общей окраске» или, точнее, одинаковому восприятию цвета. Учитываемые в модели количества шариков (молекул) и их возможных комбинаций не только фантастически велики, но и меняются в очень широких пределах, что крайне затрудняет их прямую запись и использование. К счастью, для оценки энтропии можно пользоваться не самими числами, а их логарифмами, которые и выступают в качестве меры энтропии. Напомню, что существуют два основных типа логарифмов (называемых десятичными и натуральными, которые обозначаются символами «lg» и «ln» соответственно), но мы будем пользоваться только десятичными.

Напомню также, что понятие логарифма связано со степенью его основания (в нашем случае основание равно 10), используемой для записи требуемого числа. Например,

lg 1 = 0; lg 10 = 1; lg 100 = 2; lg 1000 = 3; lg 10 000 = 4 и т. д.,

так что десятичные логарифмы чисел этого типа просто равны количеству нулей в их десятичной записи. Понятие логарифма очень легко обобщается на все остальные числа, и его обычно записывают в виде десятичной дроби, состоящей из так называемых целой части и мантиссы, как показано ниже (целая часть в записи выделена жирным шрифтом):

lg 2 = 0,301 029 995 66…

lg 53 = 1,724 275 869 60…

lg 9140 = 3,960 946 195 73…

и т. д.,

т. е. в форме, где целая часть всегда на единицу меньше количества десятичных разрядов в числе, логарифм которого она представляет. Важнейшая особенность логарифмирования состоит в том, что оно позволяет заменить операцию умножения любых чисел на сложение их логарифмов:

lg (ab) = lg a + lg b.

Именно это следует из приведенных примеров логарифмов для чисел, получаемых возведением 10 в некоторую степень, так как при умножении a = 10^А и b = 10^В можно сразу получить ab = 10^{А + В}.

Главный смысл использования логарифмов при определении энтропии связан с тем, что при объединении систем разного типа можно просто складывать значения их энтропий, т. е. энтропия обладает свойством аддитивности. Энтропия характеризуется числом размещений элементов, из которых состоит система, поэтому если мы хотим получить значение энтропии для сложной системы, составленной из двух разных независимых частей или подсистем, то нам следует просто сложить энтропии этих частей. Именно в этом смысле концепция энтропии является аддитивной. И действительно, если первой подсистеме, например, соответствует P различных комбинаций положений элементов, а второй — Q комбинаций, то число комбинаций для объединенной, составной системы будет равно произведению PQ (поскольку каждой комбинации состояний из P для первой подсистемы соответствует число Q комбинаций для второй). Таким образом, энтропия любой системы оказывается пропорциональной логарифму числа вариантов, которыми эта система может быть реализована, что непосредственно связано с указанным свойством аддитивности энтропии, и это свойство всегда сохраняется для независимых систем.

Легко заметить некоторую неясность приводимых мной аргументов, поскольку остается неопределенным само понятие «числа вариантов, которыми может быть реализована данная система». Прежде всего эта неопределенность связана с тем, что ранее при моделировании положений молекул в системе (например, в банке с краской) предполагалось, что они могут располагаться дискретно в отдельных ячейках. Это предположение является мало реалистичным в рамках классической механики Ньютона, где, строго говоря, координаты положения молекул (или их центров, неважно) могут принимать любые значения, так что число положений является бесконечным*.

Помимо этого, следует вспомнить, что у каждой отдельной молекулы может отмечаться некоторая асимметрия, т. е. она будет иметь ориентацию и поэтому должна быть охарактеризована также своей направленностью в пространстве. Кроме того, молекулы могут обладать внутренними степенями свободы (связанными, например, с искажением формы), что также должно быть как-то учтено. Иными словами, при точном подсчете числа различных состояний или конфигураций системы нам необходимо учитывать все возможные варианты ориентации и деформации молекул, что приводит к понятию о конфигурационном пространстве системы, о котором рассказывается далее.

⇐ Предыдущая 123 4 Следующая ⇒