
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вычисление стандартной неопределенности (uA) по типу А
Вычисление стандартной неопределенности (uA) по типу А
Исходными данными для вычисления являются результаты многократных измерений:
xi1,…,xini (i=1,…,m),
где ni – число измерений i-й входной величины.
Стандартную неопределенность единичного измерения i-й входной величины вычисляют по формуле:
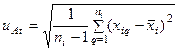 ,
,
где 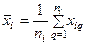 – среднее арифметическое результатов измерений i-й входной величины.
– среднее арифметическое результатов измерений i-й входной величины.
Стандартную неопределенность измерений i-й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле:
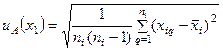
Вычисление стандартной неопределенности (uB) по типу В
Исходными данными для вычисления является следующая информация:
· данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;
· данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;
· неопределенности констант и справочных данных;
· данные поверки, калибровки, сведения изготовителя о приборе и др.
Неопределенности этих данных обычно представляют в виде границ отклонения значений величины от ее точечной оценки. При неполном знании о неопределенности некоторой i-й входной величины обычно постулируют равновероятное распределение возможных значений этой величины в указанных (нижней и верхней) границах [bi-, bi+]. При этом стандартную неопределенность, вычисляемую по типу В, определяют поформуле:
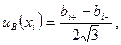
а для симметричных границ (± bi) –
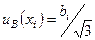 .
.
В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.
Для вычисления коэффициента корреляции используют согласованные пары результатов измерений (xil, xjl) (l=1,…nij), где nij – число согласованных результатов измерений:
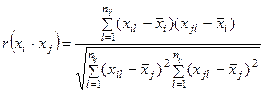 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|