
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
2. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
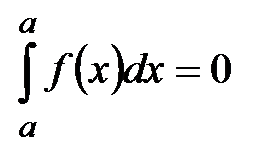 . 2°.
. 2°. 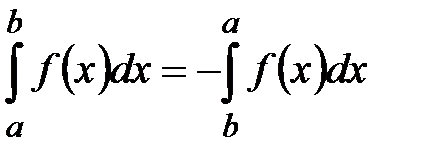 .
3°.
.
3°.  ℝ. 4°.
ℝ. 4°.  .
5°.
.
5°. 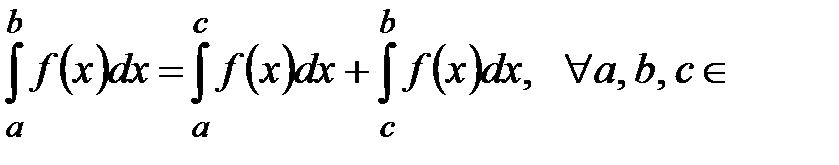 ℝ.
6°.Если
ℝ.
6°.Если  ;
; 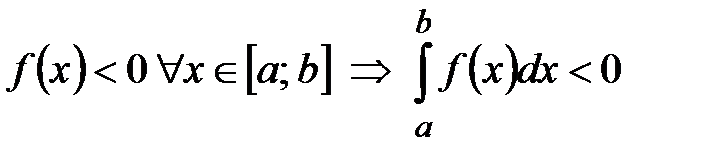 .
7°. Если
.
7°. Если 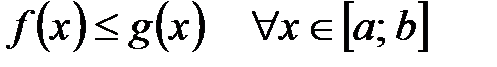 , то
, то 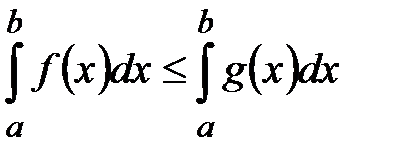 .
8°. Интегрирование по симметричному отрезку:
.
8°. Интегрирование по симметричному отрезку: 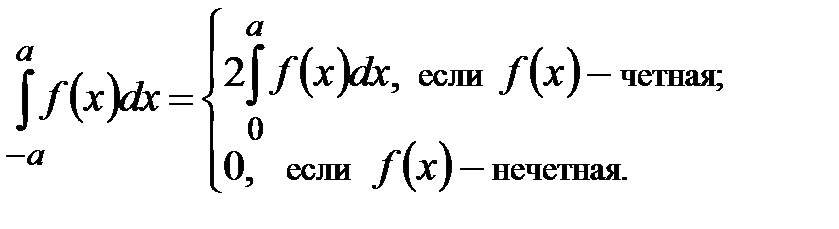 Оценка определенного интеграла:
Оценка определенного интеграла: 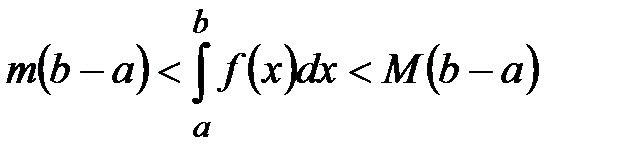 ,
где
,
где 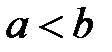 , а
, а  на
на 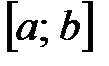 .
.
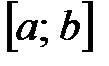 :
: 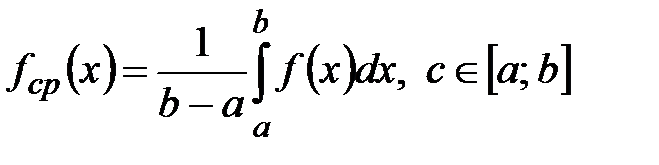 .
.
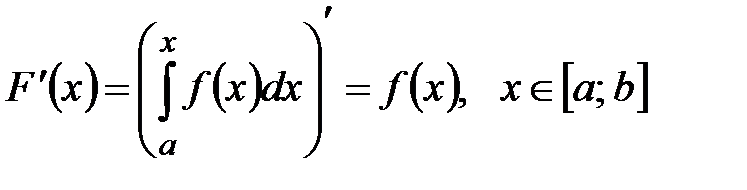 .
.
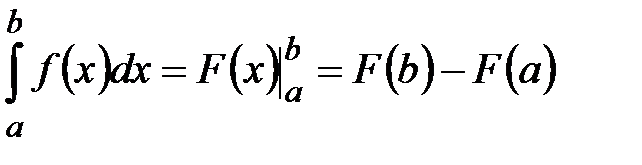 , где
, где 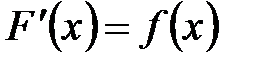 .
.
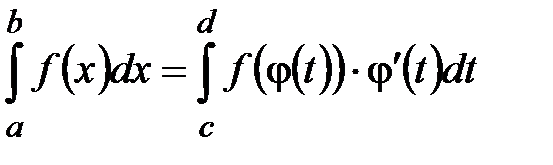 ,где
,где 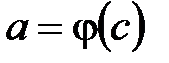 ,
, 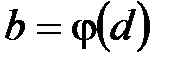 .
.
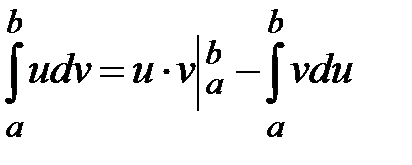 .
.
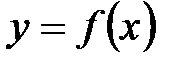 , осью
, осью 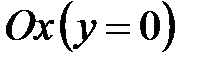 и прямыми
и прямыми 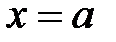 ,
, 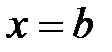 , равна:
а)
, равна:
а) 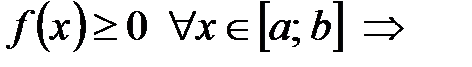
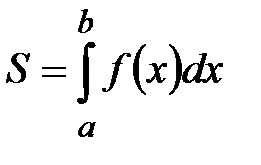 ; б)
; б) 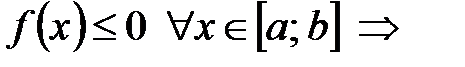
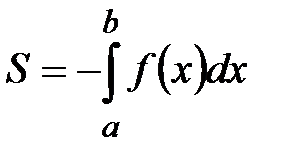 ;
в) если на
;
в) если на 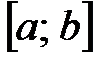 функция
функция 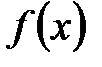 конечное число раз меняет знак, то
конечное число раз меняет знак, то 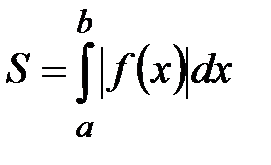 .
2. Кривыми
.
2. Кривыми 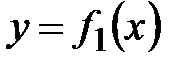 ,
, 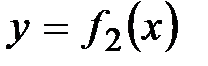
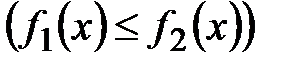 и
и 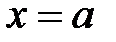 ,
, 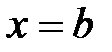 :
: 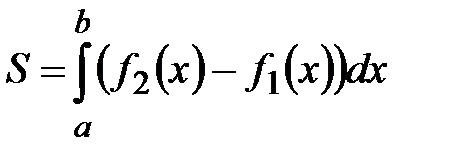 .
3.Кривой,заданнойпараметрическими уравнениями
.
3.Кривой,заданнойпараметрическими уравнениями 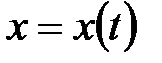 ,
,  , прямыми
, прямыми 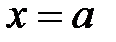 ,
, 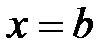 и осью
и осью 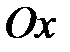 :
: 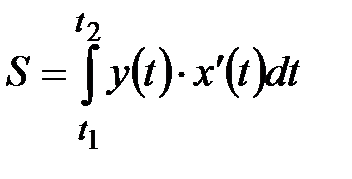 , где
, где 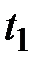 и
и 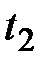 определяются из уравнений
определяются из уравнений 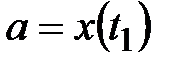 ,
, 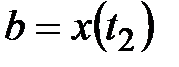 .
4. Кривой, заданной в полярных координатах уравнением
.
4. Кривой, заданной в полярных координатах уравнением 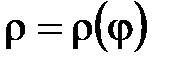 и двумя полярными лучами
и двумя полярными лучами 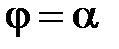 и
и 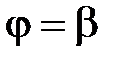
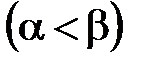 :
: 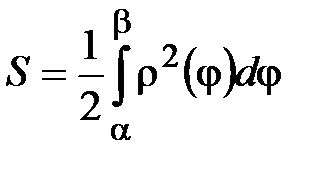 .
.
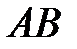 кривой
1.Если
кривой
1.Если 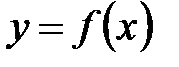 , то
, то 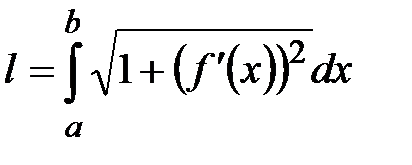 , где
, где 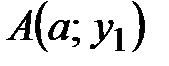 ,
, 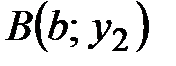 .
2.Если
.
2.Если 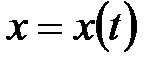 ,
, 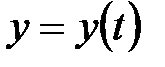 , то
, то 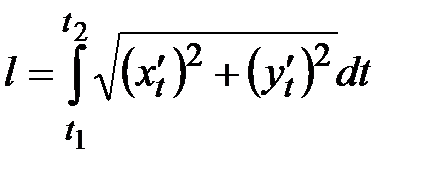 , где
, где 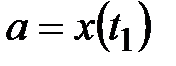 ,
, 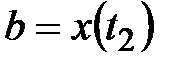 ,
, 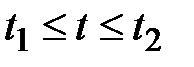 .
3.Если
.
3.Если 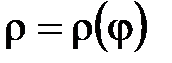 , то
, то 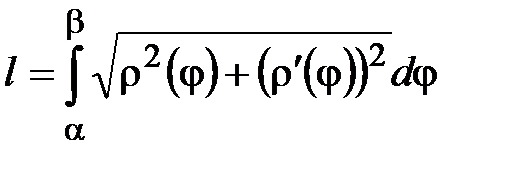 , где
, где 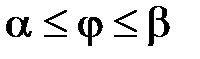 .
.
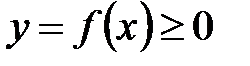 ,
, 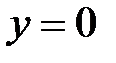 ,
, 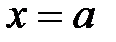 и
и 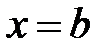 (вокруг оси
(вокруг оси 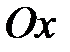 ):
): 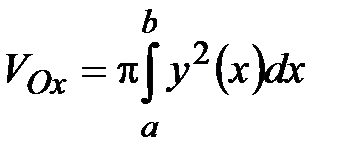 .
2.кривой
.
2.кривой 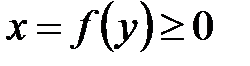 ,
, 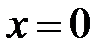 ,
, 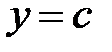 и
и 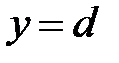 (вокруг оси
(вокруг оси 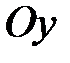 ):
): 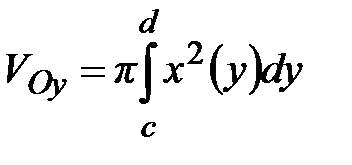 .
3.кривыми
.
3.кривыми 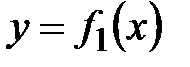 ,
, 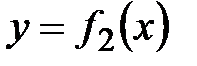
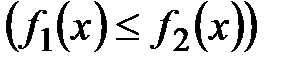 ,
, 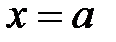 ,
, 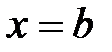 (вокруг оси
(вокруг оси 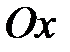 ):
):
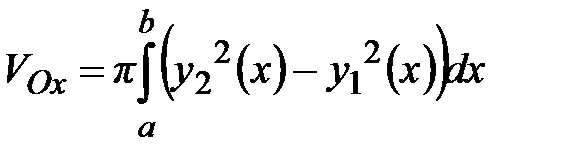 .
.
3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
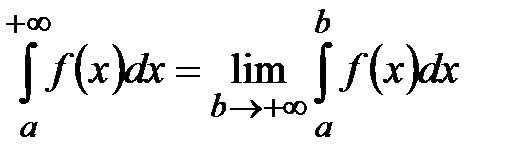 - несобственный интеграл I рода от функции
- несобственный интеграл I рода от функции 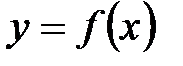 в интервале
в интервале 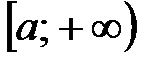 . Интеграл сходится, если существует конечный предел
. Интеграл сходится, если существует конечный предел 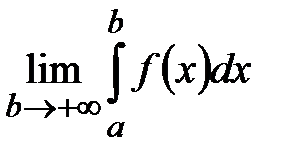 , и расходится, когда данный предел не существует.
Если функция
, и расходится, когда данный предел не существует.
Если функция 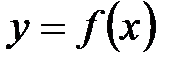 непрерывна на
непрерывна на 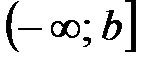 , то
, то 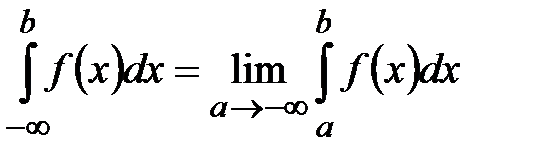 ;
Если функция
;
Если функция 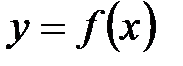 непрерывна на всей оси
непрерывна на всей оси 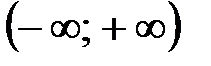 , то
, то
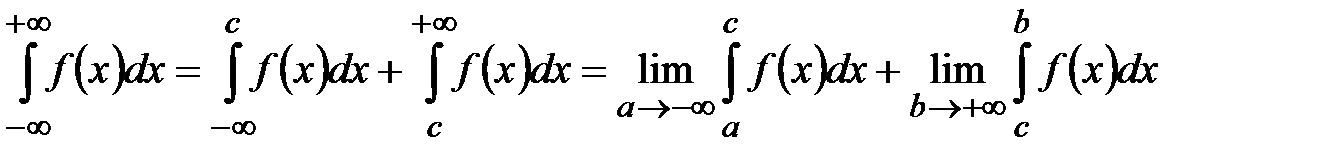 ,
где
,
где 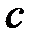 – произвольная точка действительной оси, причем интеграл не зависит от выбора точки
– произвольная точка действительной оси, причем интеграл не зависит от выбора точки 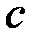 . Интеграл
. Интеграл 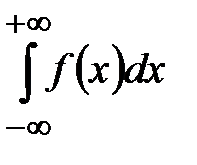 называется сходящимся, если сходятся оба определяющие его интеграла.
!!!Несобственный интеграл
называется сходящимся, если сходятся оба определяющие его интеграла.
!!!Несобственный интеграл 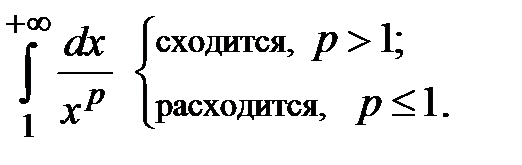
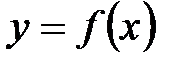 имеет на отрезке
имеет на отрезке  некоторое число точек разрыва первого рода
некоторое число точек разрыва первого рода 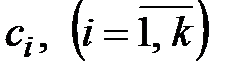 . Тогда, разбивая
. Тогда, разбивая 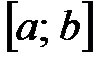 на частичныеинтервалы точками
на частичныеинтервалы точками 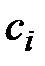 , имеем:
, имеем:
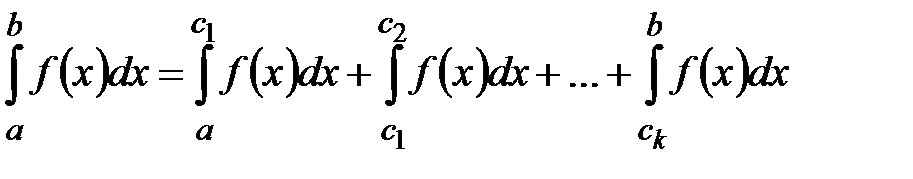 .
2.Интегралы от функций, имеющих точки разрыва второго рода
.
2.Интегралы от функций, имеющих точки разрыва второго рода
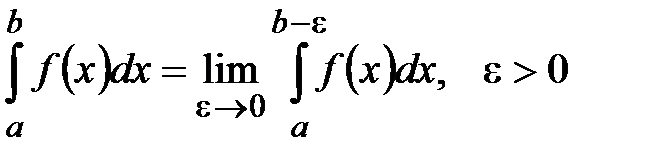 - несобственный интегралII рода от функции
- несобственный интегралII рода от функции 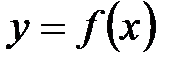 непрерывной при
непрерывной при 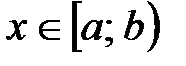 и терпящей разрыв второго рода при
и терпящей разрыв второго рода при 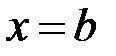 . Интегралсходится, если существует конечный предел
. Интегралсходится, если существует конечный предел 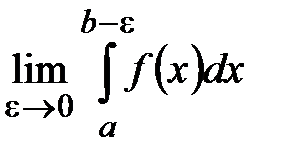 , и расходится, когда данный предел не существует.
Если
, и расходится, когда данный предел не существует.
Если 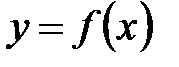 имеет разрыв при
имеет разрыв при 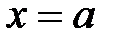 , то
, то 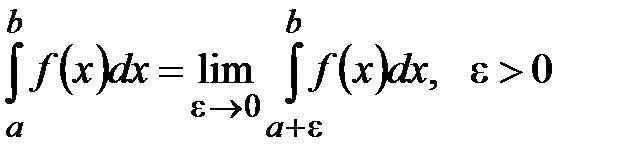 .
Если
.
Если 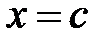 ,
, 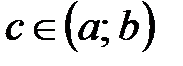 - точка разрыва функции
- точка разрыва функции 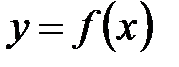 , то
, то
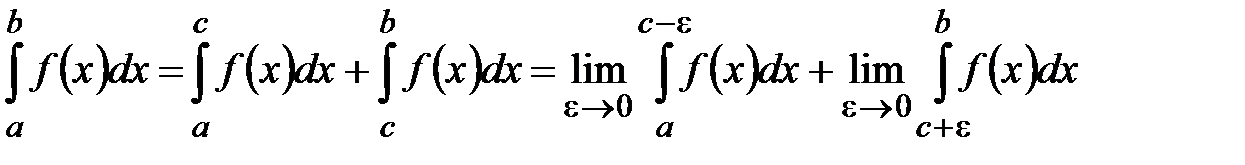 .
Интеграл
.
Интеграл 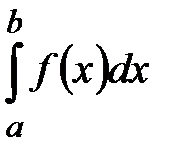 будет сходящимся, если сходятся оба интеграла из правой части равенства.
!!! Несобственный интеграл
будет сходящимся, если сходятся оба интеграла из правой части равенства.
!!! Несобственный интеграл 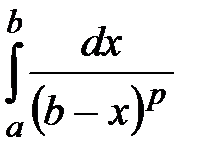 сходится при
сходится при 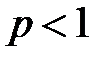 и расходится при
и расходится при 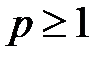 .
.