
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Стр 1 из 3Следующая ⇒
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
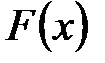 -первообразная функция для функции
-первообразная функция для функции 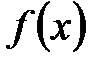 , если
, если 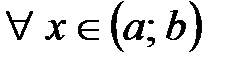
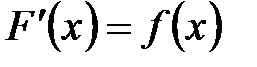 .
.
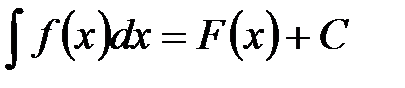 - неопределенный интеграл от функции
- неопределенный интеграл от функции 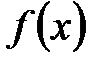 .
Свойства неопределенного интеграла
1°.
.
Свойства неопределенного интеграла
1°. 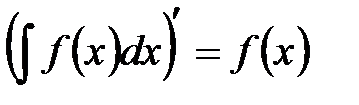 . 2°.
. 2°. 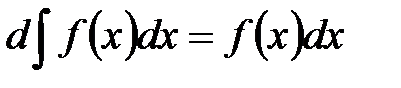 . 3°.
. 3°. 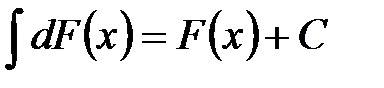 .
4°.
.
4°. 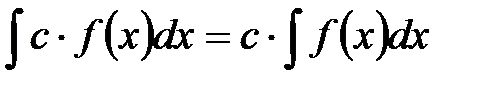 . 5°.
. 5°. 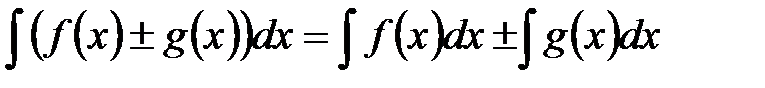 .
6°.
.
6°. 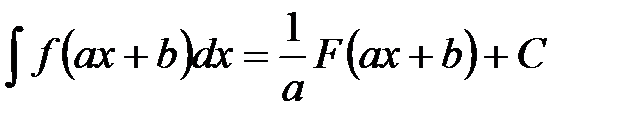 .
Простейшие неопределенные интегралы вычисляются с помощью свойств и таблицы (см. ниже).
.
Простейшие неопределенные интегралы вычисляются с помощью свойств и таблицы (см. ниже).
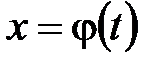 , то
, то 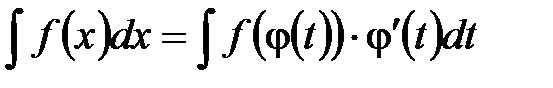 .
Иногда удобнее подбирать замену переменной в виде
.
Иногда удобнее подбирать замену переменной в виде 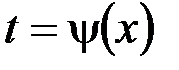 .
.
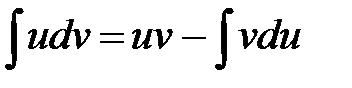 (1)
1. Формулу (1) удобно применять для интегралов вида:
А)
(1)
1. Формулу (1) удобно применять для интегралов вида:
А) 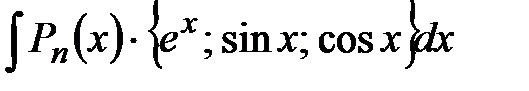 , где
, где 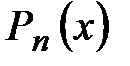 – многочлен n–й степени. При этом:
– многочлен n–й степени. При этом:
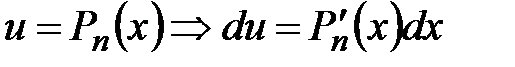 ,
, 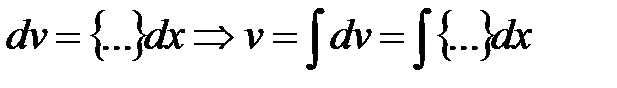 .
Б)
.
Б) 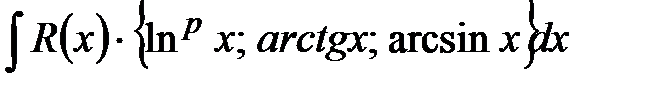 , где
, где  – дробно-рациональная функция. При этом:
– дробно-рациональная функция. При этом:
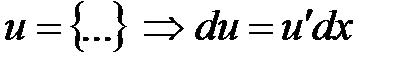 ,
, 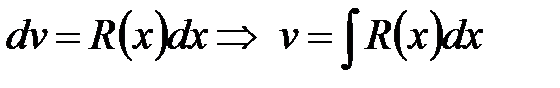 .
В)
.
В) 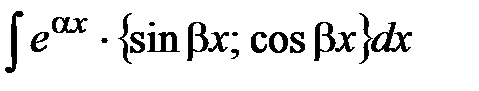 и др.
2.Иногда формулу (1) необходимо применять несколько (в случае А – п; в случае В – р) раз.
3. В ряде случаев (сл. В) применение формулы (1) приводит к решению линейного уравнения.
и др.
2.Иногда формулу (1) необходимо применять несколько (в случае А – п; в случае В – р) раз.
3. В ряде случаев (сл. В) применение формулы (1) приводит к решению линейного уравнения.
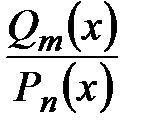 - рациональная дробь: правильная, если
- рациональная дробь: правильная, если  ;неправильная, если
;неправильная, если 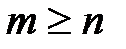 .
Если
.
Если 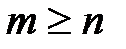 , то
, то 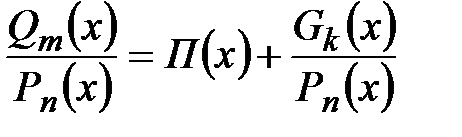 , где
, где 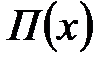 - целая часть(многочлен),
- целая часть(многочлен), 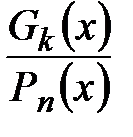
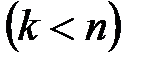 - правильная часть(правильная рациональная дробь).Данное представление может быть получено делением многочленов «уголком».
- правильная часть(правильная рациональная дробь).Данное представление может быть получено делением многочленов «уголком».
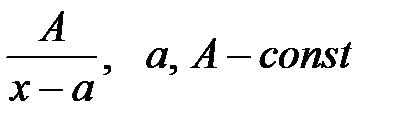 ; II.
; II. 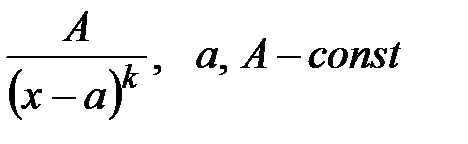 ;
III.
;
III. 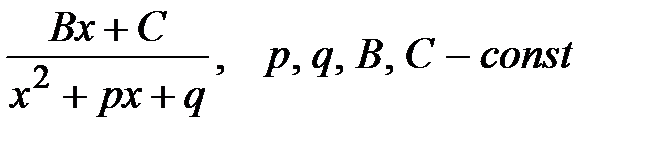 ; IV.
; IV. 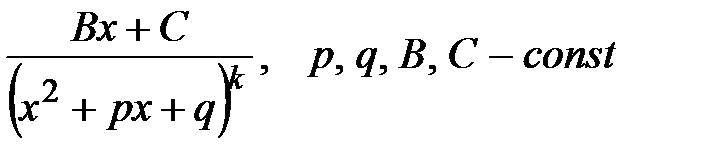 ,
где
,
где 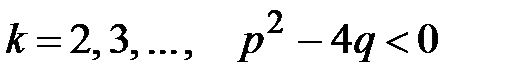 .
Любую правильную рациональную дробь можно единственным образом разложить на сумму простейших дробей. При этом каждому множителю знаменателя вида
.
Любую правильную рациональную дробь можно единственным образом разложить на сумму простейших дробей. При этом каждому множителю знаменателя вида 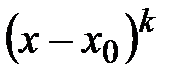 соответствует сумма
соответствует сумма 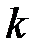 простейших дробей I и II типов; а каждому множителю знаменателя вида
простейших дробей I и II типов; а каждому множителю знаменателя вида 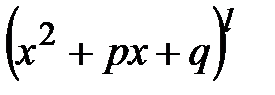 , где
, где 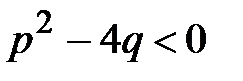 , соответствует сумма
, соответствует сумма  простейших дробей III и IV типов.
простейших дробей III и IV типов.
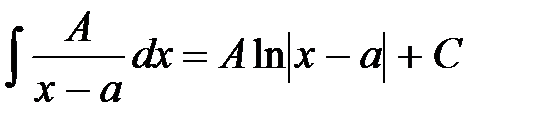 ; II.
; II. 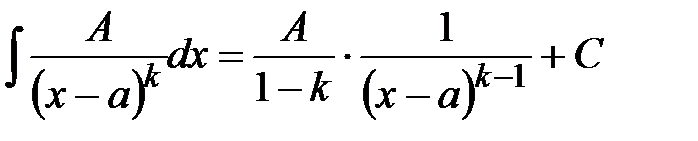 .
2) Интеграл от простейшей дроби III типаприводится к табличным интегралам с помощью замены
.
2) Интеграл от простейшей дроби III типаприводится к табличным интегралам с помощью замены 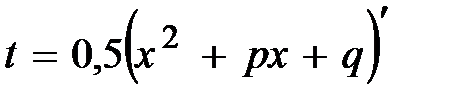 .
Или можно выделить полный квадрат в знаменателе:
.
Или можно выделить полный квадрат в знаменателе: 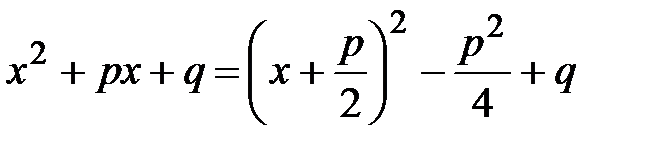 и сделать подстановку
и сделать подстановку 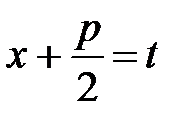 .
.
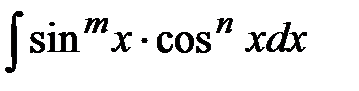 , где
, где 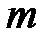 и
и 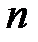 – целые числа можно вычислить следующим образом:
а) если
– целые числа можно вычислить следующим образом:
а) если 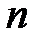 – нечетное положительное число, то применяется замена
– нечетное положительное число, то применяется замена 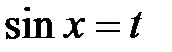 ;
б) если
;
б) если 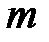 – нечетное положительное число, то делается замена
– нечетное положительное число, то делается замена 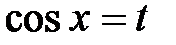 ;
в) если
;
в) если 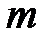 и
и 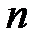 – четные положительные числа, то подынтегральную функцию преобразуют с помощью формул:
– четные положительные числа, то подынтегральную функцию преобразуют с помощью формул: 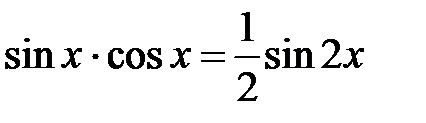 ,
,  ,
, 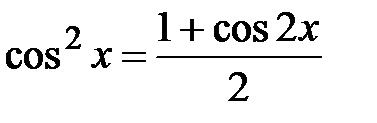 .
г) если
.
г) если 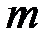 и
и 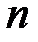 – четные числа, причем хотя бы одно отрицательно, то применяется замена
– четные числа, причем хотя бы одно отрицательно, то применяется замена 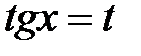 (
( 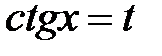 ); при этом
); при этом 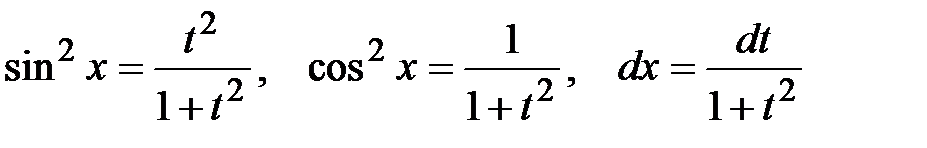 .
2) Интегралы
.
2) Интегралы 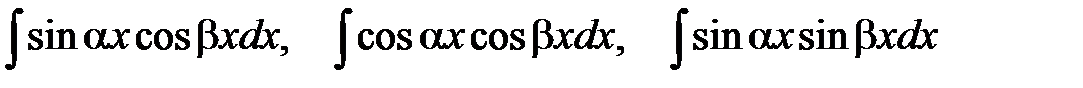 вычисляются с помощью формул:
вычисляются с помощью формул: 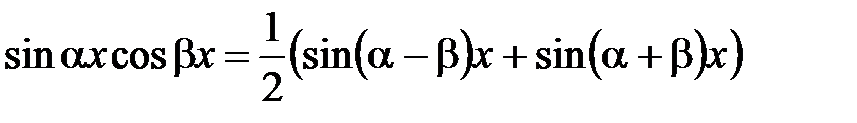 ,
,
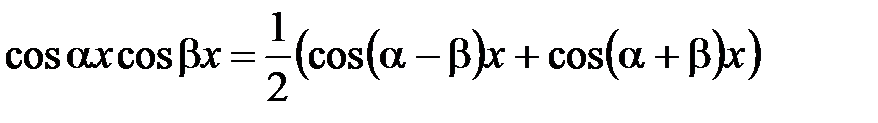 ,
, 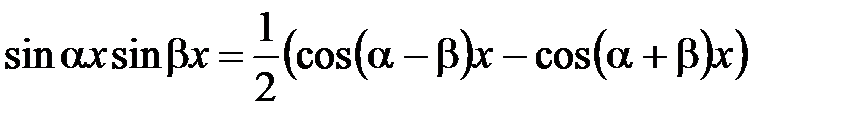 .
3) Интегралы вида
.
3) Интегралы вида 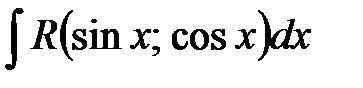 , где R – рациональная функциявычисляются с помощью универсальной тригонометрической подстановки
, где R – рациональная функциявычисляются с помощью универсальной тригонометрической подстановки
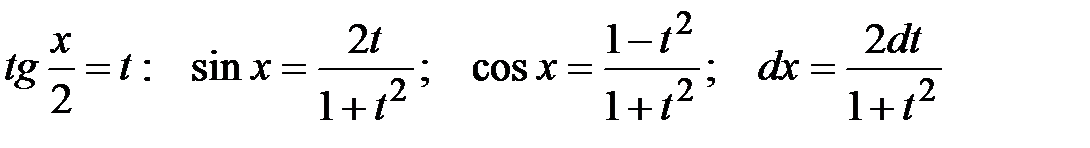 .
После такой замены интеграл приводится к интегралу от рациональной функции.
.
После такой замены интеграл приводится к интегралу от рациональной функции.
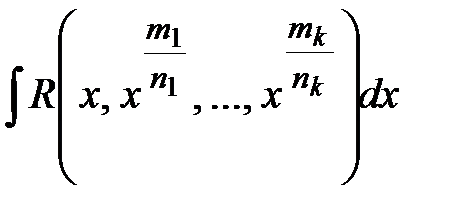 и
и 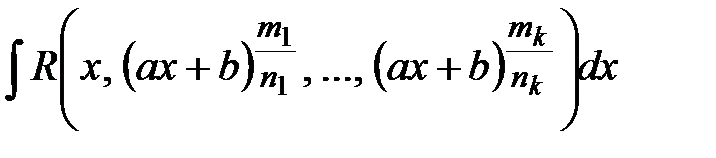 , где
, где  – рациональная функция, вычисляются заменой
– рациональная функция, вычисляются заменой 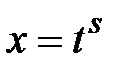 или
или 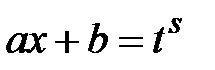 , где
, где 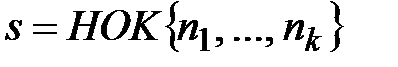 .
В частности:
.
В частности:
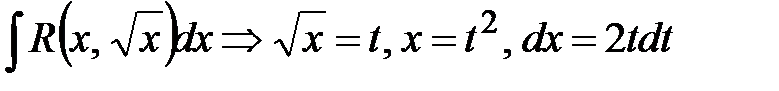 ;
; 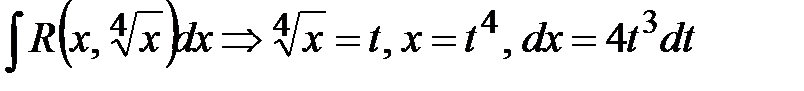 ;
; 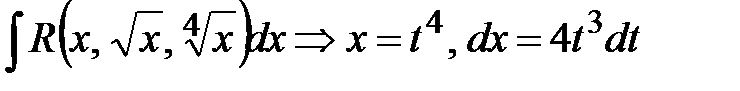 ;
; 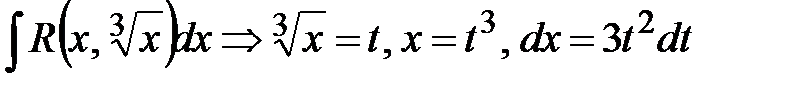 ;
; 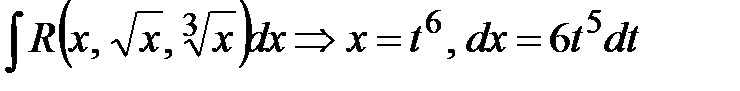 .
2) Интегралы вида
.
2) Интегралы вида 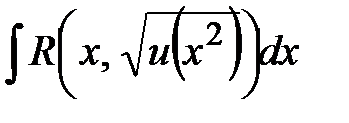 , где
, где 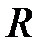 – рациональная функция, вычисляются заменами:
а) интеграл
– рациональная функция, вычисляются заменами:
а) интеграл  – замена:
– замена: 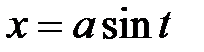 ;
б) интеграл
;
б) интеграл 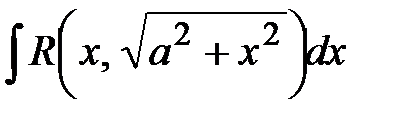 – замена:
– замена: 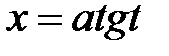 ;
в) интеграл
;
в) интеграл 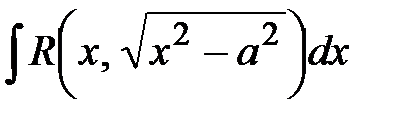 – замена:
– замена: 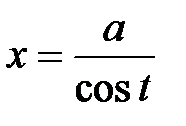 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|