по теме «Комплексные числа». по теме «Полиномы и рациональные дроби». Структура билета. Примерный вариант задания

- по теме «Комплексные числа»

Уметь работать с комплексными числами в произвольной форме записи (алгебраическая, тригонометрическая, показательная), решать уравнения и неравенства с комплексными числами и интерпретировать результаты геометрически. Производить арифметические операции, возводить в степень и извлекать корень, интерпретировать результаты геометрически.

- по теме «Полиномы и рациональные дроби»

Уметь применять теоремы Безу, Декарта к конкретным многочленам, раскладывать многочлены на множители с использованием теоремы о рациональных корнях многочлена. Выделять целую часть из рациональной дроби. Представлять правильную рациональную дробь в сумму простейших дробей.

Структура билета

8 заданий – 8 практических заданий.

Примерный вариант задания

Билет №0

1. (7 points) Найдите область определения функции .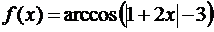

2. (15 points) Построить график, найти область определения и множество значений функции: .

3. (12 points) Найти 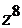, , 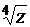если .

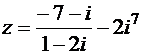4. (12 points) Представьте функцию в виде суммы многочлена и простейших рациональных дробей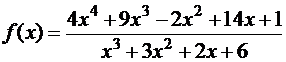

5. (15 points) Даны точки A(3,5,–1), B(0,4,1), C(1,3,3). Найдите

· угол B в треугольнике АВС;

· длину вектора 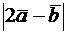, если , ;

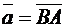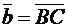· координаты точки D и длину диагонали BD в параллелограмме ABCD;

· длину вектора 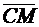, если точка М делит сторону АВ в отношении 1:2;

· числа 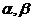, есл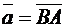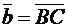и , , и .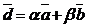

6. (20 points) Даны точки А(3, 5), B(0, 4), C(1, 3). Запишите уравнения прямых, содержащих медиану AM, высоты BH. Найдите длинувысоты BH. Найдите угол между медианой и высотой. Укажите координаты точки Н.

7. (10 points) Даны две плоскости 2x – y +2z – 6 = 0 и 3x +2y – z + 3 = 0.

· найдите угол между плоскостями.

· запишите уравнение плоскости, проходящей через точку
М(1,-2,3) и линию пересечения заданных плоскостей.

8. (15 points) Даны прямая 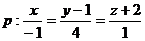и плоскость .

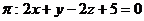· Установите взаимное расположение прямой и плоскости. Найдите расстояние между ними.

· Запишите уравнение плоскости, проходящей через прямую 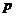, параллельно плоскости .

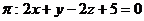· Запишите уравнение прямой 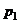, проходящей перпендикулярно плоскости через точку (1,3,‑4).

⇐ Предыдущая 12