решение СЛАУ

решение СЛАУ

Прямые методы дают алгоритм, по которому можно найти точное решение систем линейных алгебраических уравнений. Итерационные методы основаны на использовании повторяющегося процесса и позволяют получить решение в результате последовательных приближений.

Некоторые прямые методы:

* Метод Гаусса

* Метод Гаусса — Жордана

* Метод Крамера

* Матричный метод

* Метод прогонки (для трёхдиагональных матриц)

* Разложение Холецкого или метод квадратных корней (для положительно-определённых симметричных и эрмитовых матриц)

Итерационные методы устанавливают процедуру уточнения определённого начального приближения к решению. При выполнении условий сходимости они позволяют достичь любой точности просто повторением итераций. Преимущество этих методов в том, что часто они позволяют достичь решения с заранее заданной точностью быстрее, а также позволяют решать большие системы уравнений. Суть этих методов состоит в том, чтобы найти неподвижную точку матричного уравнения

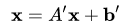
эквивалентного начальной системе линейных алгебраических уравнений. При итерации 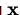в правой части уравнения заменяется, например, в методе Якоби (метод простой итерации) приближение, найденное на предыдущем шаге:

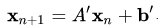
Итерационные методы делятся на несколько типов, в зависимости от применяемого подхода:

* Основанные на расщеплении:

* Вариационного типа:

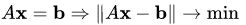
* Проекционного типа:

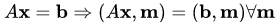
Среди итерационных методов:

* Метод Якоби (метод простой итерации)

* Метод Гаусса — Зейделя

* Метод релаксации

* Многосеточный метод

* Метод Монтанте

* Метод Абрамова (пригоден для решения небольших СЛАУ)

* Метод обобщённых минимальных невязок

* Метод бисопряжённых градиентов

* Стабилизированный метод бисопряжённых градиентов

* Квадратичный метод бисопряжённых градиентов

* Метод квази-минимальных невязок (QMR)

* Метод вращений[2]

классификация СЛАУ.

Система линейных алгебраических уравнений (линейная система, также употребляются аббревиатуры СЛАУ, СЛУ) — система уравнений, каждое уравнение в которой является линейным — алгебраическим уравнением первой степени. В классическом варианте коэффициенты при переменных, свободные члены и неизвестные считаются вещественными числами, но все методы и результаты сохраняются (либо естественным образом обобщаются) на случай любых полей, например, комплексных чисел.

⇐ Предыдущая 12