
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функция , ее свойства и график
Функция , ее свойства и график
Определение: Функция вида 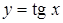 , где
, где 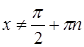 , где
, где 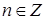 называется тангенсом
называется тангенсом
Так как тангенс периодическая функция с периодом 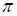 , то можно построить график в промежутке
, то можно построить график в промежутке 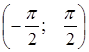 , тогда на остальных промежутках
, тогда на остальных промежутках 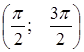 ,
, 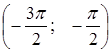 и т.д. график будет выглядеть так же.
и т.д. график будет выглядеть так же.
| х | 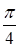
| 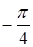
| |
| y | –1 |
Для удобства построения возьмем 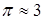 , е за 1 – две клетки.
, е за 1 – две клетки.
График не может пересекать вертикальные прямые 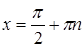 , поэтому для удобства нарисуем их пунктиром.
, поэтому для удобства нарисуем их пунктиром.
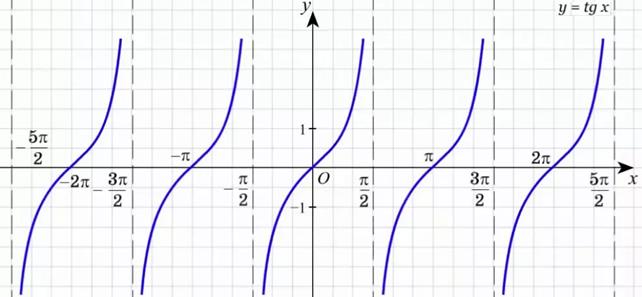
График функции 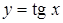 называется тангенсоидой.
называется тангенсоидой.
Свойства:
1. 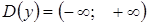 , кроме
, кроме 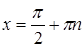 , где
, где 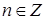
2. 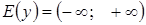
3. Функция непрерывна на области определения
4. Нечетная функция, так как 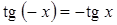
5. Периодическая, с периодом 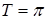 , так как
, так как 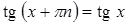 , где
, где 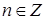
6. Нули функции: 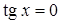 при
при 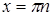 , где
, где 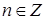
7. Промежутки знакопостоянства:
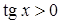 при
при 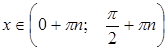 , где
, где 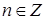
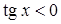 при
при 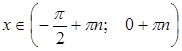 , где
, где 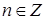
8. Функция немонотонная:
функция возрастает при 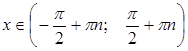 , где
, где 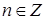
промежутков убывания нет.
9. Функция неограниченная.
Функция , ее свойства и график
Определение: Функция вида 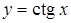 , где
, где 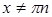 , где
, где 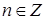 называется котангенсом
называется котангенсом
Так как котангенс периодическая функция с периодом 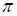 , то можно построить график в промежутке
, то можно построить график в промежутке 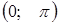 , тогда на остальных промежутках
, тогда на остальных промежутках 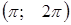 ,
, 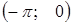 и т.д. график будет выглядеть так же.
и т.д. график будет выглядеть так же.
| х | 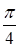
| 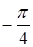
| |
| y | –1 |
Для удобства построения возьмем 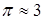 , е за 1 – две клетки.
, е за 1 – две клетки.
График не может пересекать вертикальные прямые 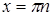 , поэтому для удобства нарисуем их пунктиром.
, поэтому для удобства нарисуем их пунктиром.
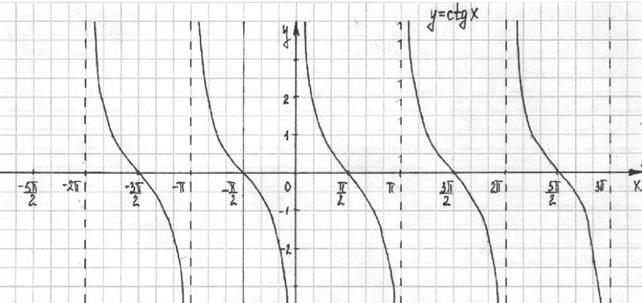
График функции 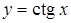 называется тангенсоидой.
называется тангенсоидой.
Свойства:
1. 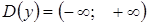 , кроме
, кроме 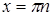 , где
, где 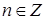
2. 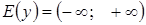
3. Функция непрерывна на области определения
4. Нечетная функция, так как 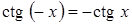
5. Периодическая, с периодом 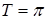 , так как
, так как 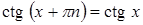 , где
, где 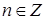
6. Нули функции: 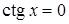 при
при 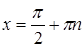 , где
, где 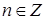
7. Промежутки знакопостоянства:
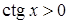 при
при 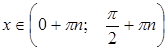 , где
, где 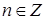
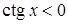 при
при 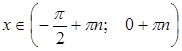 , где
, где 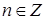
8. Функция немонотонная:
функция убывает при 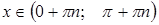 , где
, где 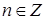
промежутков возрастания нет.
9. Функция неограниченная.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|