Хелпикс

Главная

Контакты

Случайная статья



уровень.. уровень.. ПРАКТИЧЕСКАЯ РАБОТА №2. Геометрический смысл производной.. Теоретический материал.. Алгоритм составления уравнения касательной. Порядок выполнения работы.. Изучите примеры решения задач.. вариант. уровень.

⇐ ПредыдущаяСтр 2 из 2


2 уровень.

6.  Найдите угол между касательной к графику функции 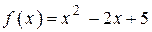 в точке с абсциссой

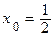    и осью абсцисс.    

7. Касательная к графику функции 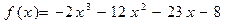образует с  положительным

направлением оси абсцисс угол 450. Найдите координаты точки касания.

 

3 уровень.

8. Касательная к графику функции 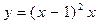параллельна оси Ох, но не совпадает с ней. Найдите

координаты точки касания.

 

а б в г

 


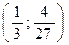
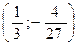
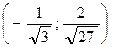
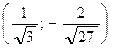
ПРАКТИЧЕСКАЯ РАБОТА №2

Геометрический смысл производной.

Цель: -научиться применять понятие и уравнение касательной при решении практических

          задач.

Теоретический материал.

       

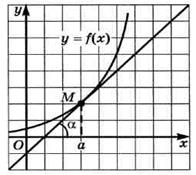
            Алгоритм составления уравнения касательной

                 

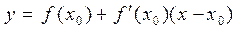
1. Обозначить абсциссу точки касания буквой   х0.

2. Вычислить .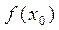

3. Найти 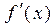и вычислить .

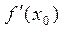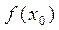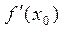4. Подставить найденные числа х0, и  в

       формулу.

Порядок выполнения работы.

1)Изучите примеры решения задач.

2. Прямая 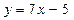 параллельна  касательной к графику функции 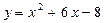.Найдите

абсциссу точки касания.

Решение: Параллельные прямые имеют одинаковый угловой коэффициент. Найдём производную

            функции и приравняем её к угловому коэффициенту касательной:

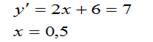
Эта точка не является общей для графика функции и прямой, значит прямая 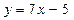   не совпадает с касательной.

Ответ: 0,5

2 вариант

1    уровень.

1. Угловой коэффициент касательной к графику функции 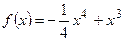 в точке с абсциссой

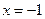  равен:                        а) 3; б) 4; в) 7; г) .

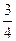2. Угловой коэффициент касательной к графику функции 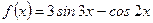 в точке с абсциссой

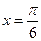 равен:                           а) 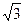; б) 10; в) 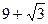; г) 6.

3. Найдите тангенс угла наклона касательной к графику функции y = 2x – x2 в точке с абсциссой

х0 = - 2.

4. Дана функция 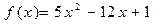.Найдите координаты точки её графика, в которой угловой

коэффициент касательной к нему равен 3.

5. К функции 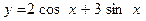 проведены касательные в точках с абсциссам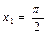и и .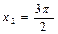

   Являются ли эти касательные параллельными прямыми?

2 уровень.

 6.  Найдите угол между касательной к графику функции 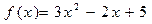 в точке с абсциссой

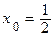      и осью абсцисс.      

 7. Найдите абсциссу точки графика функции 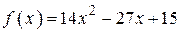, в которой касательная

наклонена под углом  450  к  оси  абсцисс.               

 

3 уровень.

 

8. Выберите координаты точки, через которую проходит касательная, проведённая к графику

функции 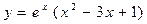в точке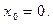

 

а б в г

 

        


⇐ Предыдущая12
  

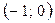
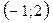
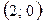
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.