
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Методические указания по практическим и семинарским занятиям по математике для студентов 1 курса
Методические указания по практическим и семинарским занятиям по математике для студентов 1 курса
Уважаемые студенты!
1. Внимательно изучите теоретический материал по теме занятия.
| Теоретический материал. |
Определение Логарифмом числа по основанию а 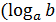 ) называется такое число с, что ) называется такое число с, что  , то есть записи , то есть записи 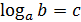 и и  равносильны. Логарифм
имеет смысл, если равносильны. Логарифм
имеет смысл, если 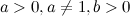 . .
|
Специальные обозначения:
1. 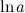

 Натуральный логарифм - логарифм по основанию , где - число Эйлера.
Натуральный логарифм - логарифм по основанию , где - число Эйлера.
2. Десятичный логарифм 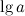 - логарифм по основанию 10.
- логарифм по основанию 10.
Свойства логарифмов:
1° 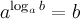 - основное логарифмическое тождество. 2°
- основное логарифмическое тождество. 2° 
3° 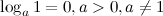
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.
4° 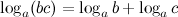 - логарифм произведения.
- логарифм произведения.
Логарифм произведения равен сумме логарифмов сомножителей.
5° 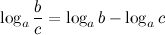 - логарифм частного.
- логарифм частного.
Логарифм частного (дроби) равен разности логарифмов сомножителей.
6° 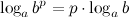 - логарифм степени.
- логарифм степени.
Логарифм степени равен произведению показателя степени на логарифм ее ос- нования.
7° 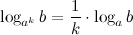
8° 
9° 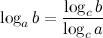 - переход к новому основанию.
- переход к новому основанию.
Примеры решения задач
Пример 1. Вычислите log 2 8 Решение: log 2 8 = 3.(т.к. 2 3 = 8)
Пример2. Вычислите log 5 25. Решение: log 5 25 = 2 Пример 3. Вычислите log224 Решение: log224 = 4
Пример 4. Вычислите 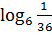 Решение:
Решение: 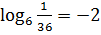
Пример 5. Вычислите 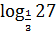 Решение:
Решение: 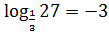
Пример 6. Вычислить  , если
, если 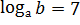
Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения: 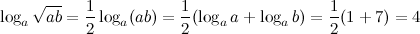
Ответ. 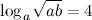
Пример7. Упростить выражение 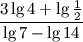
Решение. Перепишем числитель, используя свойство для степени логарифма, а знаменатель, используя свойство -логарифм произведения:
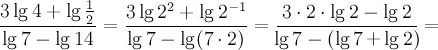
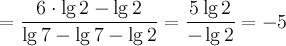 |
Примеры.
1. Доказать тождество: 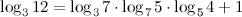
Доказательство.
Приведем все логарифмы, стоящие в правой части приведенного равенства к одному основанию 3, используя формулу для замены основания логарифма:
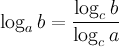
тогда выражение примет вид:
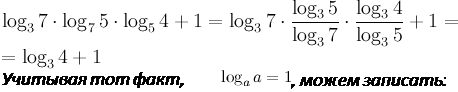

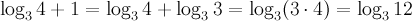
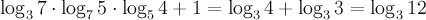 Согласно свойству суммы логарифмов получаем окончательный ответ В итоге:
Согласно свойству суммы логарифмов получаем окончательный ответ В итоге:
Что и требовалось доказать.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|