Пермский Государственный Технический Университет

Стр 1 из 3Следующая ⇒

Пермский Государственный Технический Университет

Электротехнический факультет

Кафедра автоматики и телемеханики

Вычислительные методы.

Отчет по лабораторной работе №2.

Интегрирование функций.

Выполнил: студент гр. АТ-11

Кондауров Б.А.

Проверила: Леготкина Т.С.

Цель работы:научиться применять численные методы вычисления определенных интегралов различных функций.

Задание: разработать программу вычисления определенного интеграла от функции

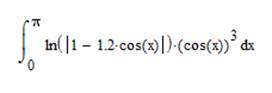
методом Симпсона и методом Чебышева с заданной погрешностью

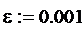
Краткая теория.

Определенный интеграл может быть вычислен аналитически для заданной функции, непрерывной на интегрируемом отрезке, если известна первообразная интегрируемой функции. В тех случаях, когда первообразная сложна и определение ее затруднительно или невозможно, или когда функция задана таблично, целесообразно вычислять определенный интеграл численными методами.

Метод Чебышева

Рассматривается стандартный интервал [-1,1], тогда

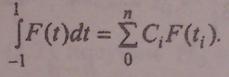
В методе Чебышева принимается, что все коэффициенты С_i, имеют равное значение С.

C = 2/(n + 1)

где (n + 1) - степень полинома, заменяющего F(t).

Значения t_i, определяются из решения системы

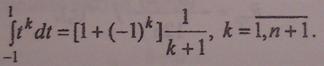
Заметим, что следует ограничиться значениями п от 1 до 8, т.к. только они приводят к вещественным корням системы.

Решения системы для разных п сведены в таблице.

При переходе к любым пределам (a, b) и к переменной х, получаем

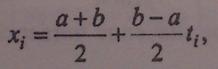
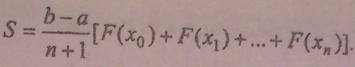
Решения системы.

12 3 Следующая ⇒