
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
График квадратичной, кубической функции
График квадратичной, кубической функции
 Парабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу.
Парабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу.
Пример 2 Построить график функции у=-х2+2х.
сначала находим вершину параболы: 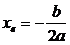 ,
, 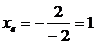 . Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
. Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
Теперь находим другие точки, при этом пользуемся симметричностью параболы.
| х | -2 | -1 | |||||
| у | -8 | -3 | -3 | -8 |
 Выполним чертеж:
Выполним чертеж:
Для квадратичной функции у=ax2+bx+c (а≠0) справедливо следующее: Если a>0, то ветви параболы направлены вверх. Если a<0, то ветви параболы направлены вниз.
Кубическая парабола
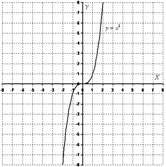 Кубическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам:
Кубическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам:
| х | -2 | -1 | |||
| у | -8 | -1 |
Гипербола
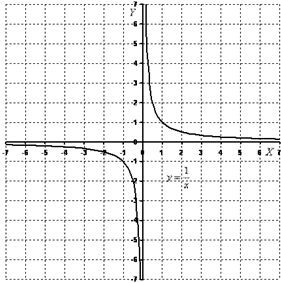 Общий вид
Общий вид 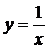 . Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.
. Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.
Выполним чертеж:График функции вида 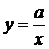 (а≠0) представляют собой две ветви гиперболы.
(а≠0) представляют собой две ветви гиперболы.
Еслиа>0, то гипербола расположена в первой и третьей координатных четвертях. Если а<0, то гипербола расположена во второй и четвертой координатных четвертях.
Пример 3. Построить правую ветвь гиперболы 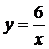 .
.
значения х выгодно подбираем так, чтобы делилось нацело:
| х | ||||
| у |
Выполним чертеж:

Практический материал
Построить графики функций:
1) у=x2+2x+3;
2) 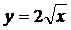 ;
;
3) 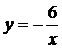 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|