
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сфера и шар.
3. Сфера и шар.
Сфера-это фигура, состоящая из всех точек пространства, удалённых от данной точки на данном расстоянии.
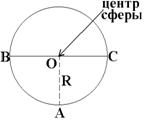
Точка О называется центром сферы, R-радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы.
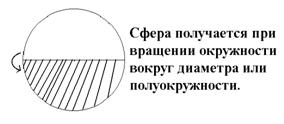
Шар-это фигура, состоящая из всех точек пространства, находящихся на расстоянии не большем данного от данной точки (или фигура, ограниченная сферой).
Уравнение сферы.
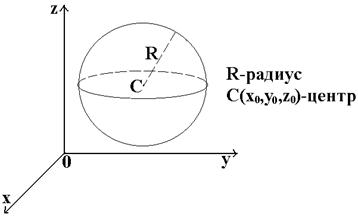
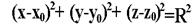
Теорема. Всякое сечение шара плоскостью есть круг, центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.
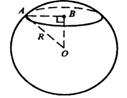
1) Наибольший радиус сечения получается когда секущая плоскость проходит через центр шара. Круг, получаемый в этом случае, называется большим кругом.
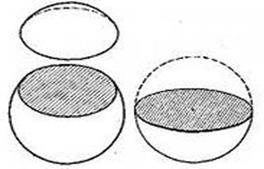
2) Сечения, равноотстоящие от центра шара, равны.
3) Из двух сечений, неодинаково удалённых от центра шара, то, которое ближе к центру, имеет больший радиус.
Касательная плоскость к сфере.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
Теорема: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
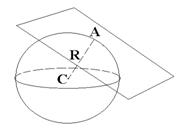
Теорема: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
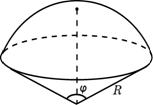
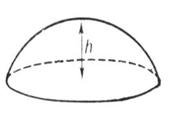
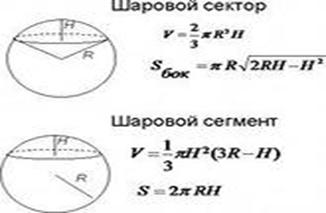
Сегмент шара Сектор шара
Шар
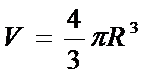
Сфера
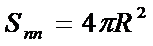
. 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|