
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Т11. Тела вращения. Объемы и площади поверхностей.
Т11. Тела вращения. Объемы и площади поверхностей.
1.Цилиндр.
Цилиндр-это фигура, состоящая из двух кругов, совмещаемых параллельным переносом и всех отрезков, соединяющих соответствующие точки этих кругов.
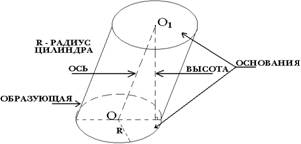
Свойства:
1. Основания равны и параллельны (из опр.).
2. Образующие равны и параллельны(из свойств параллельного переноса, по свойству параллельных плоскостей).
Цилиндр называется прямым, если образующие перпендикулярны основанию.
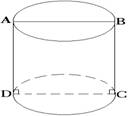
В прямом цилиндре : ось =высота = образующая.
Сечения:
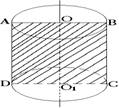
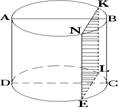
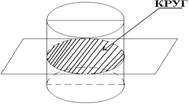
Осевое сечение , плоскостью, параллельной оси, плоскостью, параллельной основаниям
Вписанный и описанный цилиндр:
Призма называется вписанной в цилиндр(описанной около цилиндра), если основание её равные многоугольники, вписанные (описаны) в основание цилиндра.
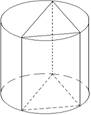
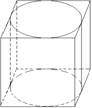
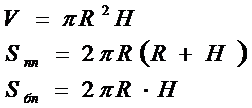
2. Конус
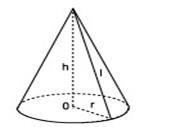
Конусом (точнее, круговым конусом) называется тело, которое состоит из круга — основания конуса, точки, не лежащей в плоскости этого круга,— вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания. Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.
Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом.
Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси
Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.
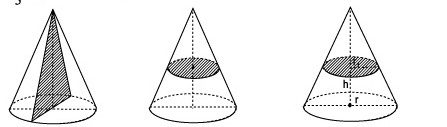
Сечения:
1. плоскостью, содержащей вершину и проходящей через основание;
2. осевое сечение;
3, 4. плоскостью, параллельной основанию

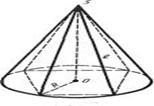
Пирамидой, описанной около конуса(вписанной в конус), называется пирамида, у которой основанием служит многоугольник, описанный (вписанный) около основания конуса, а вершина совпадает с вершиной конуса . Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
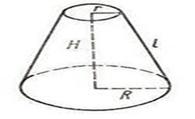
Усеченный конус–часть конуса, полученная усечением конусаплоскостью, параллельной основанию. Усеченный конус может быть получен вращением прямоугольной трапеции вокруг стороны, перпендикулярной основаниям.
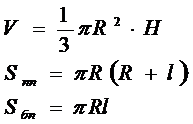
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|