Gauss's Law

The Effects of Magnetic Fields

We have seen that magnetic fields are created by charge in motion. Magnetic interactions are fundamentally interactions between moving charged particles. These interactions are described by the vector magnetic field, denoted by B. A particle with charge q moving with velocity v in a magnetic field B experiences a force F that is perpendicular to both v and B. The SI unit of magnetic field is the tesla (1T = 1N/(A·m). This basic principle will underlie much of what follows in your study of electromagnetism. The operation of electric motors, generators, transformers, and an endless variety of industrial instruments requires an understanding of the magnetic field. The major concepts are summarized below.

A magnetic field can be represented graphically by magnetic field lines. At each point a magnetic field line is tangent to the direction of B at that point. Where field lines are close together the field magnitude is large, and vice versa. Magnetic flux Ф_B through an area is defined in an analogous way to electric flux (Ф_B = ∫B·dA). The SI unit of magnetic flux is the weber (1Wb = 1T· m²). The magnetic flux density Bin a region of a magnetic field is the number of flux lines that pass through a unit of area perpendicular to the flux.B = Ф/A_┴ = Ф/Asinθ, where Ф – flux, Wb. A- unit area, m². θ – angle that plane of area makes with flux. B – magnetic flux density, T (1T = 1 Wb/ m² ).

The magnetic flux density Bis proportional to the magnetic field intensity H. The constant of proportionality is the permeability of the medium in which the field exist. B = Ф/A_┴ = μH. For a vacuum μ₀ = 4π • 10^-7 T • m/A.The relative permeability μ_r is the ratio of μ/ μ₀. We can write: B = μ₀ μ_rH. A magnetic field of flux density equal to 1T will exert a force of 1N on a charge of 1C moving perpendicular to the field with a velocity of 1m/s. F = qvBsinθ (Lorenz’s force); B = F / qvsinθ. The direction of the magnetic force is given by the right-hand-screw rules. The forceFon a wire carrying a current I at an angle θ with a flux density B is given by: F = BIlsinθ, where l is the length of the conductor. Using Ampere’s law to find the magnetic field. Equations for many common magnetic fields are given below:B = μI / 2πd (Long Wire); B = μI / 2r (Center of Loop); B = μNI / 2r (Center of Coil); B = μNI /L (Solenoid).

Ampere’s law.The magnetic fields produced byunchanging currents obey Ampere’s law: ∫B · dS = μ₀I_enclosed Here, the line integral follows any closed path through which the current I_enclosed passes. This equation is known as Ampere’s law.The total current can include both positive and negative contributions, and the path does not have to be circular, just closed. The magnetic fields produced by different currents add, or superpose, just as the electric field of different charges add according to the superposition principle. A second law obeyed by the magnetic field results from the absence of magnetic equivalents to the electric charge. Because there are not magnetic charges on which magnetic field lines begin or end, magnetic field lines must close on themselves.

This fact is expressed by Gauss’ law for magnesium: for a closed surface: Ф_B = ∫_{closed surface}B ·dA = 0. This law states that the magnetic flax, Ф_B, through any closed surface is zero; equivalently, the number of the magnetic field lines that enter a closed surface is the same as the number of lines that leaves the surface. Ampere’s elaw is an important practical tool for determining magnetic fields when there is enough symmetry to allow a path choice in which the integral simplifies, as in the determination of the interior field of a long solenoid. A solenoid is a wire wound uniformly into a coil to form a tube. When current flows, a magnetic field is produced within the tube that has a constant magnitude and is aligned with the tube axis. The magnitude of interior field is: B = μ₀nI, where n is the number of windings of wire per unit length of the solenoid. Because its interior magnetic field is constant, a solenoid is to magnetism what a capacitor is to electricity.

When there is not enough symmetry to allow Ampere’s law to be used to determine the magnetic field produced by a given configuration of currents, the Biot-Savart law can be used instead. According to this law, the magnetic field dB produced by a segment of wire dl that carries a current I at a displacement r from the segment is given by: dB = μ₀I dl x r /4π r³.

14Gauss’ Law. Application of Gauss’s Law

Gauss's Law

The total of the electric flux out of a closed surface is equal to the charge enclosed divided by the permittivity.

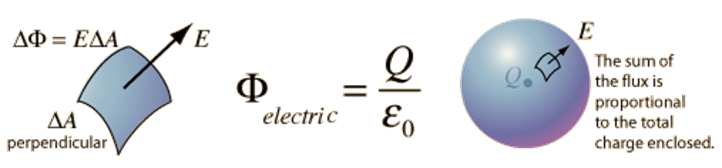
The electric flux through an area is defined as the electric field multiplied by the area of the surface projected in a plane perpendicular to the field. Gauss's Law is a general law applying to any closed surface. It is an important tool since it permits the assessment of the amount of enclosed charge by mapping the field on a surface outside the charge distribution. For geometries of sufficient symmetry, it simplifies the calculation of the electric field. Another way of visualizing this is to consider a probe of area A which can measure the electric field perpendicular to that area. If it picks any closed surface and steps over that surface, measuring the perpendicular field times its area, it will obtain a measure of the net electric charge within the surface, no matter how that internal charge is configured. Applications of Gauss' Law

Gauss' law is a powerful tool for the calculation of electric fields when they originate from charge distributions of sufficient symmetry to apply it.

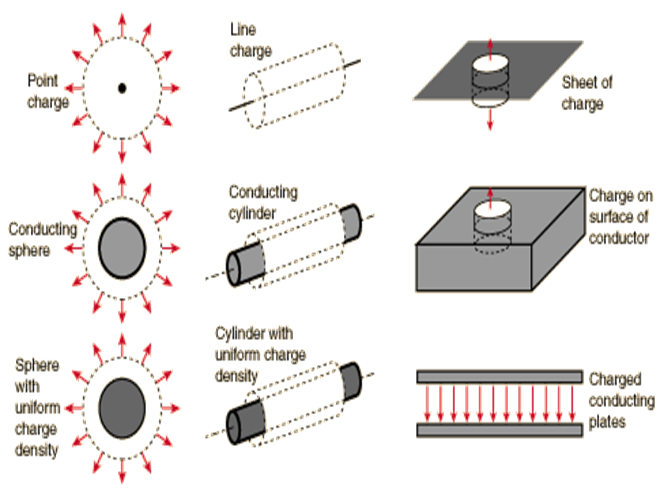
If the charge distribution lacks sufficient symmetry for the application of Gauss' law, then the field must be found by summing the point charge fields of individual charge elements.

⇐ Предыдущая 12