
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Численное интегрирование. Пример
Численное интегрирование
Пример
Даны значения функции в заданных точках:
f(-2)=11; f(-1)=1; f(0)=1; f(1)=5; f(2)=31
Требуется найти определенный интеграл этой функции на отрезке [-2; 2] с помощью:
а) интерполяции полиномом;
б) формулы трапеций;
в) формулы Симпсона.
Ход решения
1. Находим интерполяционный полином, проходящий через заданные точки и принимающий заданные значения:
j(x)=x4+x3+x2+x+1
Находим определенный интеграл этого полинома на отрезке [-2; 2]:
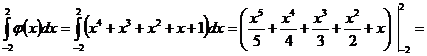
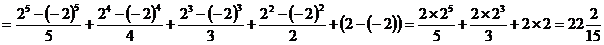 .
.
2. На каждом отрезке [xi-1; xi] имеем трапецию Ti, заданную условиями f(xi-1)=yi-1 и f(xi)=yi, площадь которой вычисляется по формуле Si=(yi+yi-1)(xi–xi-1)/2.
Формула трапеций:
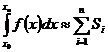 .
.
На отрезке [-2; -1] имеем трапецию T1, заданную условиями f(-2)=11 и f(-1)=1, площадь которой равна S1=(11+1)(-1–(-2))/2=6.
На отрезке [-1; 0] имеем трапецию T2, заданную условиями f(-1)=1 и f(0)=1, площадь которой равна S2=(1+1)/2=1.
На отрезке [0; 1] имеем трапецию T3, заданную условиями f(0)=1 и f(1)=5, площадь которой равна S3=(5+1)/2=3.
На отрезке [1; 2] имеем трапецию T4, заданную условиями f(1)=5 и f(2)=31, площадь которой равна S4=(31+5)/2=18.
По формуле трапеций: S1+S2+S3+S4=6+1+3+18=28.
3. Находим интерполяционный полином j1(x)=a1x2+b1x+c1, проходящий через три точки, заданные условиями: f(-2)=11, f(-1)=1 и f(0)=1.
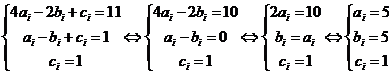
Находим определенный интеграл интерполяционного полинома j1(x)=5x2+5x+1 на отрезке [-2; 0]:
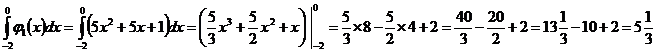
Находим интерполяционный полином j2(x)=a2x2+b2x+c2, проходящий через три точки, заданные условиями: f(0)=1, f(1)=5 и f(2)=31.
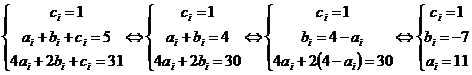
Находим определенный интеграл интерполяционного полинома j2(x)=11x2-7x+1 на отрезке [0; 2]:
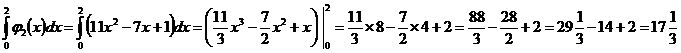
По формуле Симпсона: 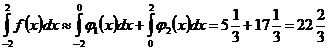 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|