
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Лекция 22. Методы интегрирования.
Лекция 22. Методы интегрирования.
22.1. Метод замены переменных.
Основную роль в интегральном исчислении играет метод замены переменной (или метод подстановки):
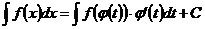 . (22.1)
. (22.1)
Предполагается, что  есть непрерывно дифференцируемая (имеющая непрерывную производную) функция на некотором интервале изменения t, а
есть непрерывно дифференцируемая (имеющая непрерывную производную) функция на некотором интервале изменения t, а 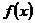 – непрерывная функция на соответствующем интервале или отрезке оси x.
– непрерывная функция на соответствующем интервале или отрезке оси x.
Докажем (22.1):
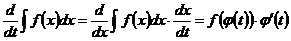 .
.
Следовательно, если ввести подстановку  , то получится первообразная от функции
, то получится первообразная от функции 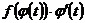 . Две первообразные отличаются на некоторую постоянную C. (22.1) доказана. ■
. Две первообразные отличаются на некоторую постоянную C. (22.1) доказана. ■
Формулу (22.1) перепишем в удобном виде:
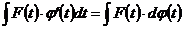 . (22.1а)
. (22.1а)
J Пример 22.1.
1) 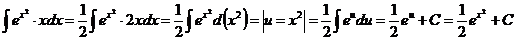 .
.
2)
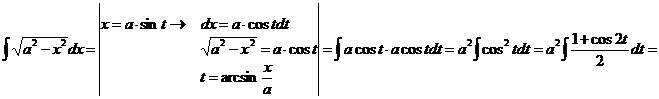
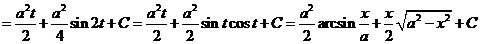 .
.
3) а) 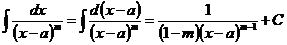
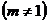 .
.
б) 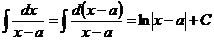 .
.
в) 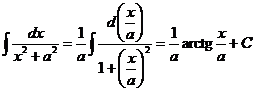
(доказательство формулы 8 таблицы интегралов лекции 21).
г) 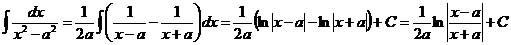
(доказательство формулы 12 таблицы интегралов лекции 21).
4) а) При 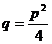
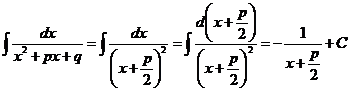 .
.
б) При 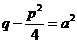 ,
, 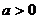 ,
,
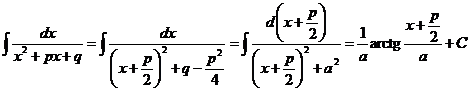 .
.
в) При 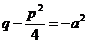 ,
, 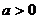 ,
,
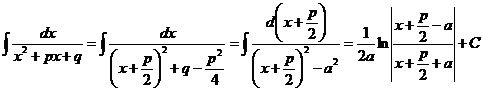 . (22.2)
. (22.2)
г) 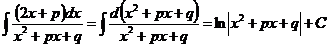 .
.
д) При 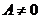
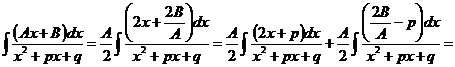
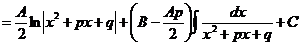 ,
,
где последний интеграл вычисляется по (22.2). J
J Пример 22.2. Вычислить заменой переменных интегралы
1) 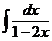 , 2)
, 2) 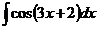 , 3)
, 3) 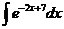 , 4)
, 4) 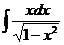 , 5)
, 5) 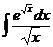 ,
,
6) 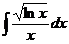 , 7)
, 7) 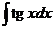 , 8)
, 8) 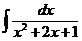 , 9)
, 9)  ,
,
10) 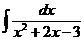 , 11)
, 11) 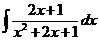 , 12)
, 12) 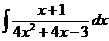 , 13)
, 13) 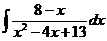 . J
. J
22.2. Метод интегрирования по частям.
♦ Теорема 22.1 (формула интегрирования по частям). Пусть 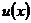 и
и 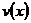 – непрерывно дифференцируемые функции. Тогда
– непрерывно дифференцируемые функции. Тогда
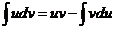 . (22.3)
. (22.3)
Доказательство. Имеем  , следовательно
, следовательно 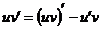 и после интегрирования получаем:
и после интегрирования получаем: 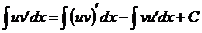 . Окончательно:
. Окончательно:
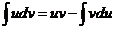 .
.
Постоянную C обычно опускают, так как в правой части формулы интегрирования по частям стоит неопределённый интеграл. ■
Интеграл 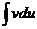 может оказаться более простым, чем
может оказаться более простым, чем 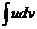 . Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на 3 группы:
. Большую часть интегралов, вычисляемых методом интегрирования по частям, можно разбить на 3 группы:
1)  ,
, 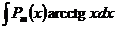 ,
,  ,
,  ,
, 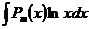 , где
, где 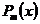 – многочлен степени m. При вычислении интегралов этой группы, необходимо за
– многочлен степени m. При вычислении интегралов этой группы, необходимо за 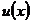 принять
принять 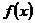 (обратную тригонометрическую функцию или логарифм) и положить
(обратную тригонометрическую функцию или логарифм) и положить 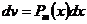 .
.
2)  ,
,  ,
, 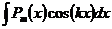 , где
, где 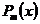 – многочлен степени m. При вычислении интегралов этой группы, необходимо принять
– многочлен степени m. При вычислении интегралов этой группы, необходимо принять 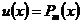 ,
, 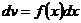 . Необходимо применить интегрирование по частям m раз.
. Необходимо применить интегрирование по частям m раз.
3) 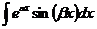 ,
, 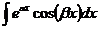 . Здесь необходимо применить двукратное интегрирование по частям, после чего искомый интеграл выражается сам через себя и находится из получающегося линейного уравнения 1‑го порядка.
. Здесь необходимо применить двукратное интегрирование по частям, после чего искомый интеграл выражается сам через себя и находится из получающегося линейного уравнения 1‑го порядка.
J Пример 22.3.1) 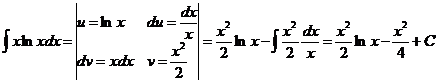 .
.
2) 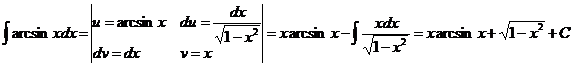 .
.
3) 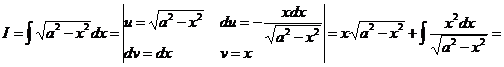
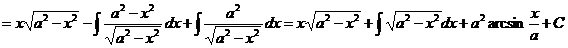 ,
,
откуда 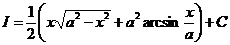 . J
. J
J Пример 22.4. 1)
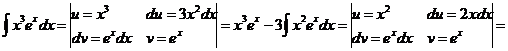
 .
.
2) 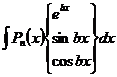 ,
,  – алгебраический многочлен. Применяем n-кратное интегрирование по частям. Так как характер первообразной легко угадывается, то эти интегралы можно вычислять методом неопределённых коэффициентов.
– алгебраический многочлен. Применяем n-кратное интегрирование по частям. Так как характер первообразной легко угадывается, то эти интегралы можно вычислять методом неопределённых коэффициентов.
Например, для 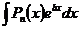 первообразная имеет вид:
первообразная имеет вид:
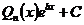 , где
, где 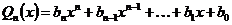 .
.
Коэффициенты находим из условия
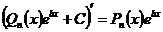
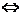
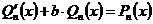 .
.
3) 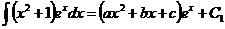 ;
;  ,
,
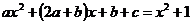 ,
, 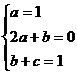
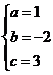
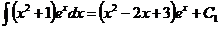 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|