Таблица № 1. «Первообразные простых функций»

ЛЕКЦИИ

Тема:«Первообразная»

Определение: функция F(x) называется первообразной для функции f(x), если выполняется равенство: F '(x) = f(x).

Общий вид первообразных для функции f(x) : F(x) + С.

Таблица № 1. «Первообразные простых функций»

f(x)	k	1 х²	1	х ⁿ	sin x	cos x	1 cos² x	1 sin² x
F'(x)	kx +c	- 1 + с х	2√х +с	х ⁿ⁺¹ n +1	- cos x+ с	sin x + с	tgx + с	- ctgx + с

Таблица № 2. «Первообразные сложных функций»

f(x)	(ах +в)ⁿ	sin(аx+в)	сos(аx+в)	а сos² (аx+в)	а sin²(аx+в)
F'(x)	(ах +в)ⁿ⁺¹ а•( n +1)	- сos(аx+в) а	sin(аx+в) а	tg(ax+в )	- сtg(ax+в)

Образцы примеров:

Пример 1. Найти общий вид первообразных для функции f(x) = x³ +1/x².

Решение:

Для функции x³ одной из первообразных будет функция x⁴/4, а для функции 1/x² одной из первообразных будет являться функция -1/x.

Ответ: F(x) = x⁴/4 – 1/x +C.

Пример 2. Найдем общий вид первообразных для функции f(x) = 5cosx +7.

Решение:

Для функции cos х одной из первообразных будет являться функция sinx, для 7 первообразная 7х.

Ответ: F(x) = 5sinx + 7х + С.

Пример 3. Найти одну из первообразных для функции y = sin(3x-2).

Решение:

Для функции y = sin(3x-2) одной из первообразных будет являться функция

- cos(3x-2).

Ответ: F(x) = - cos(3x-2) + С

________________3____________________________________________________________

Тема: «Площадь криволинейной трапеции»

у f(x) о а в х

Определение: криволинейной трапецией называется фигура, ограниченная графиком функции у= f(x), прямыми х=а, х=в и отрезком оси ОХ [а; в]. Формула для вычисления площади: в S(x) = F(x) = F(в) - F(а) а

Пример 1.Найти площадь криволинейной трапеции, ограниченной линиями: y=4x - x²; y=0;x=0; x=4.

Решение. Строим графики данных линий:
а) y=4x-x² — парабола, составим таблицу на отрезке [0; 4]:

х
у

У= 0 – это ось абсцисс, х=0 – это ось ординат, х = 4 – это прямая, параллельная оси ОУ и отстоящая вправо на 4 единицы.

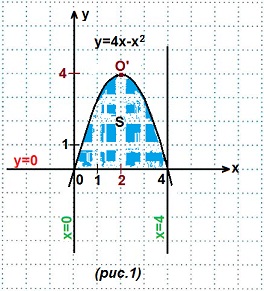
б) Находим площадь:

4 4 2

12 Следующая ⇒