Тригонометрические подстановки.

§71 Тригонометрические подстановки.

Для подынтегральных выражений, содержащих радикалы, а также их квадраты удобны тригонометрические подстановки:

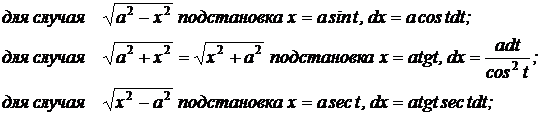
Пример 1:

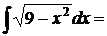
Пример 2:

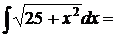
Пример 3:

§72 Некоторые интегралы, зависящие от радикалов.

Символ R(x; y) здесь и в дальнейшем обозначает дробь, числитель и знаменатель которой – многочлены относительно букв х, у. Такая дробь называется рациональной функцией двух переменных х, у. Если знаменатель постоянная величина (многочлен нулевой степени), то рациональная функция называется целой.

Аналогично определяется рациональная функция трёх переменных R(x; y; z), четырёх и т.д.

Интеграл вида

где a, b, … - рациональные числа, а p, q, r, s – постоянные величины (числовые или буквенные) приводится к интегралу рациональной функции и, значит выражается через элементарные функции, при помощи подстановки:

В частности, интеграл

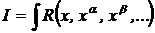
вычисляется подстановкой х=tⁿ.

Замечание:Приведение данного интеграла к интегралу рациональной функции называют рационализацией.

Пример 1:

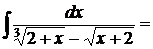
§73 Интегралы вида .

Интегралы вида:

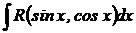
рационализируются подстановкой:

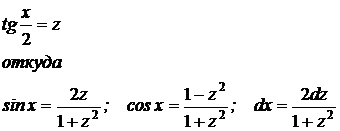
Пример 1:

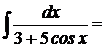
Пример 2:

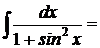
§74 Подстановки Эйлера.

Интегралы вида:

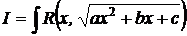
рационализируются одной из подстановок Эйлера:

Первая подстановка Эйлераприменима при a>0:

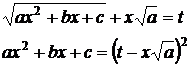
Члены, содержащие х² взаимно уничтожаются, и х (а значит, и dx) выражается через t рационально.

Третья подстановка Эйлераприменима всякий раз, когда трёхчлен 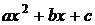имеет действительные корни, и, в частности, при a<0. Пусть корни будут х₁ и х₂, тогда полагаем

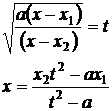
Рациональное выражение радикала находим так:

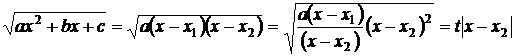
Замечание: первая и третья подстановки Эйлера достаточны, чтобы вычислить любой интеграл, рассматриваемого вида.

Вторая подстановка Эйлераприменима при c>0:

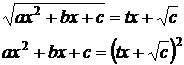
возводя в квадрат и деля затем на х, получаем рациональное выражение х через t.

⇐ Предыдущая 12