
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование некоторых тригонометрических выражений.
Лекция 16. Основные методы интегрирования.
§70 Интегрирование некоторых тригонометрических выражений.
· Для нечётных степеней sinx или cosx применимо правило:
Правило 1:
Для вычисления интегралов вида:
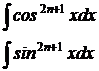
(n – целое положительное число) применим метод замены переменной – ввести вспомогательную функцию sinx в первом случае и cosx – во втором случае.
или, что то же самое применить метод внесения под знак дифференциала – выделим множитель cosx в первом случае и sinx – во втором случае и его внесём под знак дифференциала:

Пример 1:
метод прямой замены переменной:
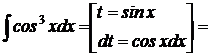
Пример 2:
метод внесения под знак дифференциала:
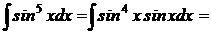
· Для чётных степеней sinx или cosx применимо правило:
Правило 2:
Для вычисления интегралов вида:
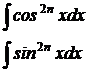
(n – целое положительное число) применим метод понижения степени по формулам:
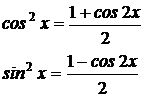
Пример 3:
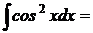
Пример 4:
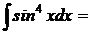
· Для произведений степеней sinx и cosx, в которых по крайней мере одна из степеней нечётна применимо правило:
Правило 3:
Для вычисления интегралов вида:
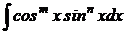
где по крайней мере одно из чисел m, n – нечётное, применим метод замены переменной – ввести вспомогательную функцию sinx, если n – нечётно и cosx, если m – нечётно.
или, что то же самое применить метод внесения под знак дифференциала, а именно, выделим множитель cosx, если m – нечётное и sinx, если n – нечётное и его внесём под знак дифференциала.
Пример 5:
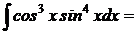
· Для произведений степеней sinx и cosx, в которых обе степени чётны применимо правило:
Правило 4:
Для вычисления интегралов вида:
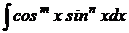
где оба числа m, n – чётны, применим метод понижения степени по формулам:
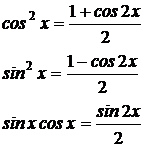
Пример 6:
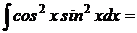
Пример 7:
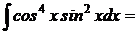
· Для произведений sinmx и cosnx, применимо правило:
Правило 5:
Для вычисления интегралов вида:

будем использовать формулы:
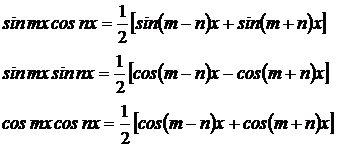
Пример 8:
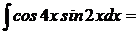
· Для степеней tgx или ctgx применимо правило:
Правило 6:
Для вычисления интегралов вида:

(n – целое число, большее 1) выделим множитель tg2x в первом случае и ctg2x – во втором случае и будем использовать формулы:
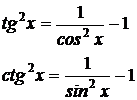
Пример 9:
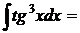
Пример 10:
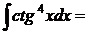
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|