
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Урок 19. Площадь треугольника. Цель деятельности учителя. I этап. Проверка домашнего задания. Теоретический опрос. II этап. Мотивация к деятельности. III этап. Изучение новой темы
Урок 19. Площадь треугольника
Цель деятельности учителя
Создать условия для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу
I этап. Проверка домашнего задания. Теоретический опрос
Цель деятельности
Ход урока
Проверить уровень усвоения формул для нахождения площади треугольника
– Повторите теорему о площади треугольника.
– Вспомните формулу для вычисления площади прямоугольного треугольника.
– Вспомните, что если высоты двух треугольников равны, то их площади соотносятся как основания.
– Решите задачи.
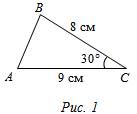
Найти: SАВС.
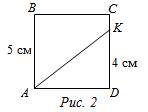
ABCD – квадрат, АВ = 5 см, KD = 4 см.
Найти: SABCK.
АВ = 10.
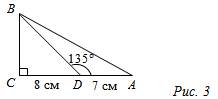
Найти: SВСА.
II этап. Мотивация к деятельности
Через решение задач подготовить учащихся к восприятию новой теоремы
(Ф)
1. 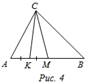
СМ – медиана ∆ABС, СK – медиана ∆АСМ.
Найти: SАСМ : SАВС; SАСМ : SВСK; SАСK : SВСK.
Ответ: 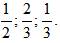
2. 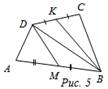
М – середина АВ, K – середина CD. ABCD – выпуклый четырехугольник.
Доказать: SМВKD = SАВСD : 2.
Доказательство: SАDВ : SМDВ = 2 : 1; SDСВ : SDKВ = 2 : 1; SАВСD = SАDВ + SDВС; SМDKВ = SМDВ + SDKВ; SАВСD : SМDKВ = 2 : 1
III этап. Изучение новой темы
Доказать теорему
об отношении площадей треугольников, имеющих по равному углу
(Ф)Теорема.Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведение сторон, заключающих равные углы. (Доказательство посмотрите в учебнике)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|