
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Комбинированное занятие № 24. Тема. Сумма и разность синусов и косинусов.. Изучение нового материала.. Сумма синусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразноста этих углов.. Разность синусов двух углов равна удвоенном
Комбинированное занятие № 24
Тема. Сумма и разность синусов и косинусов.
Цели занятия:
Образовательная - на основе повторения и обобщения ранее изученного материала вывести формулы суммы и разности синусов и косинусов; научить применять формулы при выполнении тождественных преобразований тригонометрических выражений.
Развивающая - развивать умения применять знания на практике, способствовать развитию логического мышления, воли и самостоятельности, развитие умений учебного труда (умение работать в темпе).
Воспитательная - создавать условия для воспитания интереса к изучаемой теме, воспитания мотивов учения, положительного отношения к знаниям, воспитания дисциплинированности, обеспечивать условия успешной работы в коллективе.
Ход занятия:
Изучение нового материала.
Преобразование суммы (разности) синусов двух углов в произведение.
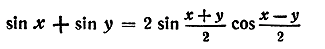 (2)
(2)
Сумма синусов двух углов равна удвоенному произведению синуса полусуммы на косинус полуразноста этих углов.
Заменяя в формуле (2) у на — у и учитывая, что sin ( — у) = — sin у, получаем:
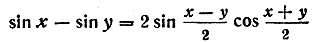 (3)
(3)
Разность синусов двух углов равна удвоенному произведению синуса полуразности на косинус полусуммы этих углов.
Примеры.
1) Сумму sin 75° + sin 15° легко вычислить без таблиц, если использовать формулу (2):
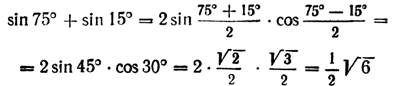
2) Разность sin 5π/12 — sin π/12 легко вычислить без таблиц, если использовать формулу (3):
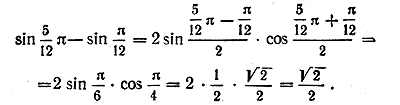
Преобразование суммы (разности) косинусов двух углов в произведение
Для суммы и разности косинусов двух углов верны следующие формулы:
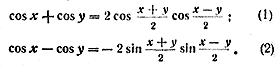
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|